The Homogeneous Cooling State

The Homogeneous Cooling State can be characterized at the kinetic or at the hydrodynamics level. We expose both the characterizations.

Kinetics of the Homogeneous Cooling State

We rewrite here the Boltzmann Equation for a 3D cooling granular gas [42,210] (see paragraph 2.2.8):

$$\begin{multline} \left( \frac{\partial}{\partial t}+L_1^0 \right)P(\mathbf{r}_1,... ...athbf{r}_1,\mathbf{v}_1,t)P(\mathbf{r}_1,\mathbf{v}_2,t) \right ] \end{multline}$$

The kinetic definition of Homogeneous Cooling State is given by the scaling ansatz for the state distribution function:

$$P(\mathbf{r},\mathbf{v},t)=nP(\mathbf{v},t)=\frac{n}{v_0^d(t)}\tilde{P}(\mathbf{c})$$ (5.1)

where $\mathbf{c}=\mathbf{v}/v_0(t)$ and $v_0(t)$ is the thermal velocity defined by $T(t)=mv_0^2(t)/2$ with $T(t)$ the temperature (defined for example in Eq. (2.116)). If the Eq. (5.2) is inserted in the Boltzmann Equation (5.1), an equation for the temperature is obtained:

$$\frac{dT}{dt}=-\frac{\Omega_d}{\sqrt{2 \pi}}mn\sigma^{d-1}v_0^3\gamma=-2\omega\gamma T$$ (5.2)

where $\Omega_d=2\pi^{d/2}/\Gamma(d/2)$ is the surface area of a $d$-dimensional unit sphere, $\omega$ is the time dependent collision frequency, while $\gamma$ is the time independent cooling rate. These last two functions are defined by:

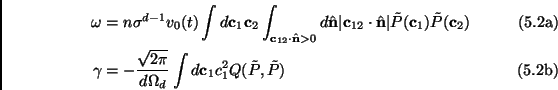and can be approximated, using the Maxwellian approximation $\tilde{P} \approx \pi^{-d/2}\exp(-c^2)$, by $\omega_0$ and $\gamma_0$ respectively, given by:

The solution of the temperature equation (5.3) reads:

$$T(t)=\frac{T(0)}{(1+\gamma_0 t/t_0)^2}=T(0)\exp(-2\gamma_0 \tau)$$ (5.5)

where $t_0=1/\omega(T(0))$ is the mean free time at the initial temperature $T(0)$ and

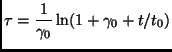$$\tau=\frac{1}{\gamma_0}\ln(1+\gamma_0+t/t_0)$$ (5.6)

is the cumulated collision number obtained from the definition $d\tau=\omega(T(t))dt$. Eq. (5.6) is known as Haff's law [103] and has been discussed in paragraph 2.4.1.

Hydrodynamics of the Homogeneous Cooling State

The hydrodynamics for the Inelastic Hard Spheres model [39,214] is described by the following equations (see section 2.4):

These equations are generally closed with constitutive relations obtained by means of expansions of kinetic equations. The results presented in this section have been obtained by van Noije, Ernst, Brito and Orza [212] and are based on the following (Navier-Stokes order) approximations:

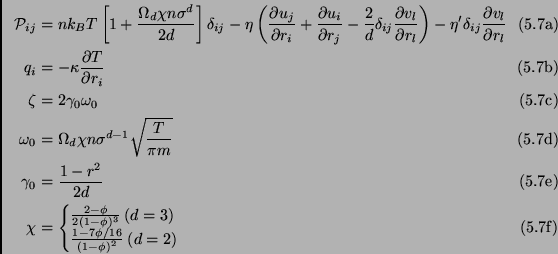with $\eta$, $\eta'$ and $\kappa$ the shear viscosity, bulk viscosity and heat conductivity respectively. The expression for the pressure correction $p=nk_BT[1+...]$ and for the collision frequency correction (which both contains the pair distribution function of hard spheres or disks at contact $\chi=g_2(r=\sigma)$) are obtained from the Enskog theory (see paragraph 2.2.6), with $\phi$ the volume fraction ( $\pi n\sigma^2/4$ if $d=2$ or $4\pi n\sigma^3/3$ if $d=3$).

The equations (5.8) are solved by the following homogeneous solution:

where $T(t)$ is the same as in Eq. (5.6).

An expansion of the kinetic equation in the inelasticity parameter $\epsilon=1-r^2\equiv 2d\gamma_0$ has shown [210,198] that $\gamma$ and $\omega$ are well approximated by $\gamma_0$ and $\omega_0$ (their Maxwellian counterparts) for almost all values of $r$.