next up previous contents
Next: The hydrodynamical limit Up: From the Liouville to Previous: The ring kinetics equations   Contents

The Boltzmann equation for granular gases

The binary collision operator $ \overline{T}_-(1,2)$, for inelastic particles, must be changed [210] according to the inelastic collision rules, Eqs. (2.41) and Eqs. (2.42). It must be noted that when $ r=1$ (elastic collisions), the two set of equations coincide, i.e. the direct or inverse collision are identical transformation. This is not true if $ r < 1$. Therefore, in the definition of the inverse binary collision operators at the end of section 2.2.1, that is $ T_-(1,2)$ and $ \overline{T}_-(1,2)$, we have put the same operator $ b_c$ that appears in the direct binary collision operators $ T_+(1,2)$ and $ \overline{T}_+(1,2)$, while in general it must be used the operator $ b_c'$ that replaces velocities with precollisional velocities (using the transformation given in Eqs. (2.42)). The adjoint of inverse binary inelastic collision operator(the only one needed in the following) therefore reads:

$\displaystyle \overline{T}_-(1,2)=\sigma^2\int_{\mathbf{V}_{12} \cdot \hat{\mat... ...thbf{n}})b_c'-\delta(\mathbf{r}_1-\mathbf{r}_2+\sigma\hat{\mathbf{n}}) \right ]$ (2.94)

Deriving from this the BBGKY hierarchy (analogue of (2.94)) and putting in the first equation of it the Molecular Chaos assumption, the Boltzmann Equation for granular gases is obtained [41,210]:

\begin{multline} \left( \frac{\partial}{\partial t}+L_1^0 \right)P(\mathbf{r}_1,... ...athbf{r}_1,\mathbf{v}_1,t)P(\mathbf{r}_1,\mathbf{v}_2,t) \right ] \end{multline}

where the primed velocities are defined in Eqs. (2.42).

This equation has been studied in the spatially homogeneous case (no spatial gradients, $ L_1^0=0$), with the Enskog correction (i.e. a multiplying factor $ \Xi(\sigma,n)$ in front of the collision integral) by Goldshtein and Shapiro [97] and by Ernst and van Noije [211]. The equation is

\begin{multline} \frac{\partial}{\partial t}F(\mathbf{v}_1,t) = \Xi(\sigma,n)\si... ...,t)F(\mathbf{v}_2',t)-F(\mathbf{v}_1,t)F(\mathbf{v}_2,t) \right ] \end{multline}

where $ F(\mathbf{v},t)=\int d\mathbf{r} P(\mathbf{r},\mathbf{v},t)$. Goldshtein and Shapiro [97] have shown that this equation admits an isotropic scaling solution which describes the so-called ``Homogeneous Cooling State'', depending on time only through the temperature $ T(t)$ defined by the relation $ \frac{3}{2}nT(t)=\int d\mathbf{v}\frac{1}{2}mv^2F(\mathbf{v},t)$:

$\displaystyle F(\mathbf{v},t)=\frac{n}{v_0^3(t)}\overline{F}\left( \frac{v}{v_0(t)} \right)$ (2.95)

with $ v_0$ defined by the relation $ T(t)=mv_0^2(t)/2$.

The scaling function solves a complicated integro-differential equation. This can be studied using an expansion in Sonine polynomials:

$\displaystyle \overline{F}(\overline{v})=f_0(\overline{v})[1+a_2S_2(\overline{v}^2)+...]$ (2.96)

where $ \overline{v}=v/v_0(t)$, $ f_0(\overline{v})=\pi^{-3/2}\exp(-\overline{v}^2)$ is the Maxwellian and $ S_2(x)=x^2/2-5x/2+15/8$ is the second Sonyne polynomial. The calculations of Ernst and van Noije [211] have shown that for $ 0.6 \leq r <1$ the coefficient $ a_2$ is very near to zero, precisely $ \vert a_2\vert \leq 0.04$ in three dimensions and $ \vert a_2\vert \leq 0.024$ in two dimensions. The decay of the temperature has also been calculated:

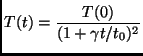$\displaystyle T(t)=\frac{T(0)}{(1+\gamma t/t_0)^2}$ (2.97)

with $ \gamma=\gamma_0(1+3a_2/16)$ (dimensionless damping rate), $ \gamma_0=(1-r^2)/2d$, and the initial Maxwellian mean free time $ t_0=1/\omega_0(T)$ ( $ \omega_0(T)$ is the collision frequency calculated with a Maxwellian with temperature $ T$), while the true collision frequency reads $ \omega(T)=\omega_0(T)(1-a_2/16)$. Monte Carlo simulations (DSMC, see Appendix A) by Brey et al. [42] of the Eq. (2.99) have shown that the temperature decay and the fourth cumulant $ a_2$ qualitatively agree with the results of Ernst and van Noije. Moreover the agreement between very dilute Molecular Dynamics simulations and Monte Carlo solutions of the Boltzmann equation in 2D have shown agreement up to moderate inelasticities ( $ r \geq 0.7$).

Ernst and van Noije [211] have also given estimates for the tails of the velocity distribution, using an asymptotic method employed by Krook and Wu [129]. This method assumes that for a fast particle the dominant contributions to the collision integral come from collisions with thermal (bulk) particles and that the gain term of the integral can be neglected with respect to the loss term. They found an exponential behavior for the tails of the scaling distribution function of velocities:

$\displaystyle \overline{f}(\overline{v}) \sim \exp(-\beta_1c)$ (2.98)

with $ \beta_1$ a constant depending on $ r$.

It is relevant that Ernst and van Noije have also studied Enskog-Boltzmann equation in the presence of a random forcing, i.e. a source of energy that acts randomly, uncorrelated and isotropically on all the particles. The homogeneous equation for this system reads:

\begin{multline} \frac{\partial}{\partial t}F(\mathbf{v}_1,t) = \Xi(\sigma,n)\si... ...\frac{\partial}{\partial \mathbf{v}_1} \right)^2F(\mathbf{v}_1,t) \end{multline}

where the velocity diffusion coefficient $ \xi_0^2$ appears, which is proportional to the rate of energy input per unit mass $ \frac{3}{2}\xi_0^2$. This equation admits a stationary homogeneous solution $ F_S(\mathbf{v})=(n/v_0^3)\overline{F}(v/v_0)$ with $ v_0$ defined as above in terms of the granular temperature $ T$. It is immediate to obtain a temperature balance

$\displaystyle \frac{dT}{dt}=m\xi_0^2-2\gamma\omega_0T.$ (2.99)

From Eq. (2.105) follows the value for the stationary temperature (if the system remains homogeneous!). The authors have also given estimates for the coefficient $ a_2$ of the Sonine expansion. Molecular dynamics by van Noije et al. [211] have shown that the predictions of the homogeneous Boltzmann equation work for $ r \geq 0.7$ and low densities. The Krook and Wu method for the asymptotic behavior of the tails of the velocity distribution.function gives

$\displaystyle \overline{f}(\overline{v}) \sim \exp(-\beta_2c^{3/2}).$ (2.100)

next up previous contents
Next: The hydrodynamical limit Up: From the Liouville to Previous: The ring kinetics equations   Contents
Andrea Puglisi 2001-11-14