The Liouville and the pseudo-Liouville equations

In order to discuss the behavior of a system of $N$ identical hard spheres (of diameter $\sigma$ and mass $m$) it is natural to introduce the phase space, i.e., a $6N-$dimensional space where the coordinates are the $3N$ components of the $N$ position vectors of the sphere centers $\mathbf{r}_i$ and the $3N$ components of the $N$ velocities $\mathbf{v}_i$. The state of the system is represented by a point in this space. We call $\mathbf{z}$ the $6N$-dimensional position vector of this point. If the positions $\mathbf{r}_i$ of the spheres are restricted in a space region $\Omega$, then the full phase space is given by the product $\Omega^N \times \Re^{3N}$

If the state is not known with absolute accuracy, we must introduce a probability density $P(z,t)$ which is defined by

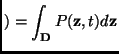$$Prob(z \in \mathbf{D} t )=\int_\mathbf{D}P(\mathbf{z},t)d \mathbf{z}$$ (2.45)

where $d\mathbf{z}$ is the Lebesgue measure in phase space and we implicitly assume that the probability is a measure absolutely continuous with respect to the Lebesgue measure.

The mean value of a dynamical observable $A(\mathbf{z})$ can be calculated from either the following expressions:

$$\int_{\infty}d\mathbf{z}P(\mathbf{z},0)A(\mathbf{z}(t))=\int_{\infty}d\mathbf{z}P(\mathbf{z},t)A(\mathbf{z})$$ (2.46)

which are respectively the Lagrangian and Eulerian averages (analogous to the Heisemberg and Schroedinger averages in quantum mechanics). In Eq. (2.47) the time dependence of the observable $A$ and of the distribution $P$ is due to the time evolution operator $S_t$ (also called streaming operator, that is $A(\mathbf{z}(t)) \equiv S_t(\mathbf{z})A(\mathbf{z})$. Considering the equivalence in Eq. (2.47) as an inner product implies that

$$P(\mathbf{z},t)=S_t^\dagger P(\mathbf{z},0)$$ (2.47)

where $S_T^\dagger$ is the adjoint of $S_t$.

In a general system (not necessarily made of hard spheres) with conservative and additive interactions, the force between the particle pair $(ij)$ is $\mathbf{F}_{ij}=-\partial V(r_{ij})/\partial \mathbf{r}_{ij}$ so that the time evolution operator is given by:

$$S_t(\mathbf{z})=\exp[tL(\mathbf{z})]=\exp\left[ t \sum_iL_i^0-t\sum_{i<j}\Theta(ij) \right]$$ (2.48)

where the Liouville operator $L(\mathbf{z})... \equiv \{H(\mathbf{z}),...\}$ is the Poisson bracket with the Hamiltonian, so that

and $S_t(\mathbf{z})$ is a unitary operator, $S_t^\dagger=S_{-t}$, while $L^\dagger=-L$. In Eq. (2.49) the evolution operator $S_t$ has been divided into a free streaming operator $S_t^0=\exp[t\sum_i L_i^0]$ which generates the free particle trajectories, plus a term containing the binary interactions among the particles.

Finally the Liouville equation is obtained writing explicitly Eq. (2.48):

$$\frac{\partial}{\partial t}P(\mathbf{z},t)= \left( -\sum_iL_i^0 + \sum_{i<j}\Theta(ij) \right)P(\mathbf{z},t)$$ (2.50)

which is an expression of the incompressibility of the flow in phase space.

In the specific case of identical hard spheres, the interaction among particles is defined by Eq. (2.30). It can be shown that this kind of interaction carries no contraction of phase space at collision, i.e.

$$P(\mathbf{z}',t)=P(\mathbf{z},t)$$ (2.51)

where $\mathbf{z}'$ and $\mathbf{z}$ are the phase space points before and after a collision. This can be considered a form of detailed balance law. It is important to stress that $\mathbf{z}' \neq \mathbf{z}$: a collision represents a time discontinuity in the velocity section of phase space. In particular we use the elastic collision model defined in this list of prescriptions (it coincides with the collision rule for smooth hard spheres, see Eq. (2.33)):

these relations conserve the total momentum and the total energy of the system.

To derive the Boltzmann equation, the collisions events $\mathbf{z} \to \mathbf{z}'$ are considered as boundary conditions and the Liouville Equation (2.51) is restricted to the interior of the phase space region $\Lambda \equiv \Omega^N \times \Re^{3N}- \Lambda_{ov}$ where

$$\Lambda_{ov}=\left\{\mathbf{z} \in \Omega^N \times \Re^{3N} \mid ... ....,N\} \: (i \neq j) : \vert\mathbf{r}_i-\mathbf{r}_j\vert<\sigma \right\}$$ (2.53)

is the set of phase space points such that one or more pairs of spheres are overlapping. With this conditions, the Liouville equation reads:

This version of the Liouville equation is time-discontinuous: this means that formal perturbation expansions used in usual many-body theory methods cannot be applied to it.

An alternative master equation for the probability density function in the phase space can be derived [83]. The streaming operator $S_t$ for hard spheres is not defined for any point of the phase space $\mathbf{z} \in \Lambda_{ov}$. In the calculation of the average (2.47) of physical observables, this is not a problem, as the streaming operators appears multiplied by $P(\mathbf{z},0)$ which is proportional to the characteristic function $X(\mathbf{z})$ of the set $\Lambda$ (the characteristic function is $1$ for points belonging to the set and 0 for points outside of it). In perturbation expansions it is safer to have a streaming operator defined for every point of the configurational space. A standard representation, defined for all points in the phase space, has been developed for elastic hard spheres and is based on the binary collision expansion of $S_t(\mathbf{z})$ in terms of binary collision operators. The binary collision operator is defined in terms of two-body dynamics through the following representation of the streaming operator for the evolution of two particles:

$$S_t(1,2)=S_t^0(1,2)+\int_0^td\tau S_\tau^0(1,2)T_+(1,2)S_{t-\tau}^0(1,2)$$ (2.55)

with $S_t^0=\exp(tL_0)$ the free flow operator and a collision operator

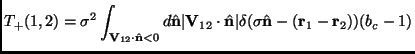$$T_+(1,2)=\sigma^2\int_{\mathbf{V}_{12} \cdot \hat{\mathbf{n}} <0}... ...athbf{n}}\vert\delta(\sigma\hat{\mathbf{n}}-(\mathbf{r}_1-\mathbf{r}_2))(b_c-1)$$ (2.56)

where $b_c$ is a substitution operator that replaces $\mathbf{v}_1,\mathbf{v}_2$ with $\mathbf{v}_1',\mathbf{v}_2'$ (see Eqs. (2.53)).

The Eq. (2.56) is a representation of the evolution of two particles as a convolution of free flow and collisional events. Noting that $T_+(1,2)S_\tau^0(1,2)T_+(1,2)=0$ for $\tau>0$ (two hard spheres cannot collide more than once), Eq. (2.56) can be put in the form

$$S_t(1,2)=\exp \left\{t[L_0(1,2)+T_+(1,2)]\right\}$$ (2.57)

that can be generalized to the N-particle streaming operator (here considered for the case of an infinite volume):

$$S_{\pm t}(\mathbf{z})=\exp \left\{\pm t[L_0(\mathbf{z}) \pm \sum_{i<j}T_\pm (i,j)]\right\}$$ (2.58)

where

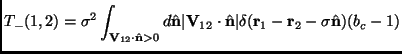$$T_-(1,2)=\sigma^2\int_{\mathbf{V}_{12} \cdot \hat{\mathbf{n}} >0}... ...\mathbf{n}}\vert\delta(\mathbf{r}_1-\mathbf{r}_2-\sigma\hat{\mathbf{n}})(b_c-1)$$ (2.59)

Equation (2.59) defines the so-called pseudo-streaming operator. In order to write an analogue of the Liouville Equation (2.51), the adjoint of $S_{\pm t}$ is needed: its definition is identical to that in Eq. (2.59) but for the binary collision operators which must be replaced by their adjoints:

$$\overline{T}_\pm(1,2)=\sigma^2\int_{\mathbf{V}_{12} \cdot \hat{\m... ...a\hat{\mathbf{n}})b_c-\delta(\mathbf{r}_1-\mathbf{r}_2+\sigma\hat{\mathbf{n}})]$$ (2.60)

Finally the pseudo-Liouville equation can be written:

$$\frac{\partial}{\partial t}P(\mathbf{z},t)= \left( -\sum_iL_i^0 + \sum_{i<j}\overline{T}_-(ij) \right)P(\mathbf{z},t).$$ (2.61)

This equation is the analogue of Eq. (2.51) for the case of hard core potential (hard spheres). In this sense it replaces Eq. (2.55) and will be used in the following, precisely in paragraph 2.2.7, to derive kinetic equations different from the ones discussed just below.