Hard spheres

Hard spheres are one of the simplest models of molecular fluids and have represented for many years the testing ground for the predictions of the kinetic theory, thanks to the pioneering efforts of physicists who have developed hard spheres simulations on the old computers which were huge in encumbrance and very small in power (the work of Alder and Wainwright is considered the foundation of this subject [2,3,1,4,5]). Nowadays liquids and gases are almost always simulated with different tools and models (e.g. Lenard-Jones potentials or others), i.e. typically soft spheres models. Nevertheless the study of granular materials has again awakened the interest in hard spheres molecular dynamics, as the geometric character of the grain-grain interaction seems to be better modeled by an hard core interaction. Here we define the hard core potential and give expressions for the quantities calculated in the previous paragraphs.

Two hard spheres in 3D (hard disks in 2D, hard rods in 1D) of diameters $\sigma_1$ and $\sigma_2$ interact by means of a discontinuous potential

of the form:

$\begin{subequations}\begin{align}U(r) & = 0 \;\; (r>\sigma_{12}) \ U(r) & = \infty \;\; (r<\sigma_{12}) \end{align}\end{subequations}$

where $\sigma_{12}=(\sigma_1+\sigma_2)/2=r_m$ is the distance of the centers of the spheres at contact. The potential in Eq. (2.30) can be taken as a definition of hard spheres systems. In this case the deflection angle is given by:

$\displaystyle \chi=2 \arccos \left(\frac{b}{\sigma_{12}} \right)$

(2.31)

and the dependence from the initial relative velocity disappears (only geometry determines the deflection angle).

The differential scattering cross section for hard spheres is calculated from Eq. (2.22) obtaining a very simple formula: $s(V_{12},\chi)=\sigma^2/4$ which can be integrated over the entire solid angle space giving an expression for the total cross section $S=\pi \sigma^2$ . This result is consistent with the physical intuition of the cross section: it is the average of the areas of influence of the scatterer in the planes perpendicular to the approaching velocities of the incident particles.

Other interesting quantities to be easily calculated for hard spheres systems are the transport cross sections (see definition in Eq. (2.24)). The first two are given here:

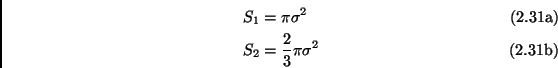$\begin{subequations}\begin{align}S_1 &= \pi\sigma^2 \ S_2 &= \frac{2}{3}\pi \sigma^2 \end{align}\end{subequations}$

**Figure 2.2:** The collision between two elastic hard spheres
$\includegraphics[clip=true,width=12cm,keepaspectratio]{smooth_hard_spheres.eps}$

Finally we give a definition of smooth hard spheres (we consider this model as a paradigm for granular gases): smoothness is the absence of irregularities on the surface of the spheres, i.e. the instantaneous collision does not change the rotational degrees of freedom of the spheres at contact. Therefore, in the study of smooth hard spheres systems, a complete description of the dynamics requires only the positions of the centers $\mathbf{r}$ and their velocities $\mathbf{v}$ . In particular the collision is an instantaneous transformation of the velocities of two particles

and

at contact which are ``reflected'' with the following rule (see Fig. fig_collision_2):

$\displaystyle \mathbf{v}'_i$	$\displaystyle =\mathbf{v}_i-\frac{2m_2}{m_1+m_2}\hat{\mathbf{n}}[\hat{\mathbf{n}} \cdot (\mathbf{v}_i-\mathbf{v}_j)]$	(2.33)
$\displaystyle \mathbf{v}'_j$	$\displaystyle =\mathbf{v}_j+\frac{2m_1}{m_1+m_2}\hat{\mathbf{n}}[\hat{\mathbf{n}} \cdot (\mathbf{v}_i-\mathbf{v}_j)]$	(2.34)

where $\hat{\mathbf{n}}=(\mathbf{r}_i-\mathbf{r}_j)/\vert\mathbf{r}_i-\mathbf{r}_j\vert$ and the primes denote the velocities after the collision. This collision rule conserves momentum and kinetic energy. It only changes the direction of the component of the relative velocity of the particles in the direction of $\hat{\mathbf{n}}$ (normal component), leaving unchanged the tangential component.