Statistics of the elastic collision

The concept of mean free path was introduced in 1858 by Rudolf Clausius [65] and paved the road to the development of the kinetic theory of gas. For the sake of simplicity (and coherently with the rest of this work, as well as with the literature on granular gases) we consider a single species gas composed of hard spheres, all having the same diameter $\sigma$ and mass $m$ (see [62] or [98]).

The mean free time is the average time between two successive collisions of a single particle. We define $\nu dt$ the probability that a given particle suffers a collision between time $t$ and $t+dt$ ($\nu$ is called collision frequency) and assume that $\nu$ is independent of the past collisional history of the particle. The probability $f_{time}dt$ of having a free time between two successive collisions larger than $t$ and shorter than $t+dt$ is equal to the product of the probability that no collision occurs in the time interval $[0,t]$ and the probability that a collision occurs in the interval $[t,t+dt]$:

$$f_{time}(t)dt=P_{time}(t)\nu dt$$ (2.17)

where $P_{time}(t)$ is the survival probability, that is the probability that no collisions happen between 0 and $t$, and can be calculated observing that $P_{time}(t+dt)=P_{time}(t)P_{time}(dt)=P_{time}(t)(1-\nu dt)$ so that $dP_{time}/dt=-\nu P_{time}$, i.e. $P_{time}(t)=e^{-\nu t}$.

Finally one can calculate the average of the free time using the probability density $f_{time}(t)$:

$$\tau=\int_0^\infty dt t f_{time}(t)=\int_0^\infty dt t \nu e^{-\nu t}= \frac{1}{\nu}.$$ (2.18)

With the same sort of calculations an expression for the mean free path, that is the average distance traveled by a particle between two successive collisions, can be calculated. One again assumes that there is a well defined quantity (independent of the collisional history of the particle) $\alpha d\mathit{l}$ which is the probability of a collision during the travel between distances $\mathit{l}$ and $\mathit{l}+d\mathit{l}$. The survival probability in terms of space traveled is $P_{path}(\mathit{l})=e^{-\alpha \mathit{l}}$ and the probability density of having a free distance $\mathit{l}$ is $f_{path}(\mathit{l})=e^{-\alpha \mathit{l}} \alpha$ so that the mean free path is given by:

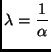$$\lambda=\frac{1}{\alpha}$$ (2.19)

The other important statistical quantity in the study of binary collisions is the so-called differential scattering cross section $s$ which is defined in this way: in a unit time a particle suffers a number of collisions which can be seen as the incidence of fluxes of particles coming with different approaching velocities $\mathbf{V}_{12}$ and scattered to new different departure velocities $\mathbf{V}_{12}'$. Given a certain approaching velocity $\mathbf{V}_{12}$ the incident particles arrive with slightly different impact parameters (due to the extension of the particles), and therefore are scattered in a solid angle $d\Omega'$. If $I_0$ denotes the intensity of the beam of particles that come with an average approaching speed $\mathbf{V}_{12}$, which is the number of particles intersecting in unit time a unit area perpendicular to the beam ( $I_0=nV_{12}$ with $n$ the number density of the particles), then the rate of scattering $dR$ into the small solid angle element $d\Omega'$ is given by

$$\frac{dR}{d\Omega'}=I_0 s(\mathbf{V}_{12},\mathbf{V}_{12}')$$ (2.20)

where $s$ is a factor of proportionality with the dimensions of an area (in $3D$) which is called differential cross section and depends on the relative velocity vectors before and after the collisions. The total rate of particles scattered in all directions, $R$ is the integral of the last equation:

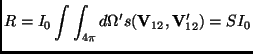$$R=I_0\int\int_{4\pi}d\Omega' s(\mathbf{V}_{12},\mathbf{V}_{12}')=S I_0$$ (2.21)

and defines the total scattering cross section $S$.

In the case of a spherically symmetric central field of force the differential cross section is a function only of the modulus of the initial relative velocity $V_{12}$, the angle of deflection $\chi$, and the impact parameter $b$ which in turn, once fixed the potential $U(r)$, is a function only of $\chi$ and $V_{12}$, that is $s=s(V_{12},\chi)$. In particular it can be easily demonstrated that

$$s(V_{12},\chi)=-\frac{b(V_{12},\chi)}{\sin \chi} \frac{db}{d\chi}.$$ (2.22)

The case of inverse power interaction potential is of interest also for the study of cross sections: a very famous result in this framework is the Rutherford formula that concerns the differential cross section for the case $a=2$ (scattering of an electron by an atomic nucleus):

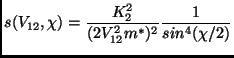$$s(V_{12},\chi)=\frac{K_2^2}{(2V_{12}^2m^*)^2} \frac{1}{sin^4(\chi/2)}$$ (2.23)

where $K_2=e^2/4\pi\epsilon_0$ (for the electron charge $e$ and the vacuum permittivity $\epsilon_0$).

In addition to the differential and total scattering cross sections, in non-equilibrium transport theory several other cross sections are defined:

$$S_k(V_{12})=\int_0^{2\pi}d\epsilon \int_0^\pi d\chi \sin \chi (1-cos^k \chi)s(V_{12},\chi)$$ (2.24)

where $k$ is a positive integer (n=1,2,....). For instance, the transfer of the parallel component of the particle momentum is proportional to $1-\cos \chi$ (see Eq. (2.10)) and therefore $S_1$ is related to the transport of momentum and plays an important role in the study of diffusion. Moreover, viscosity and heat conductivity depend on $S_2$.

To conclude this paragraph we recall that the collision frequency defined at the beginning is strictly tied to the total scattering cross section by the relation

$$\nu=nS\overline{V_{12}}$$ (2.25)

where $n$ is the average density of the gas and $\overline{V_{12}}$ is an average of the relative velocities. Generally speaking (in the framework of a non-equilibrium discussion) $n$ and $\overline{V_{12}}$ are averages taken in space-time regions in which equilibrium can be assumed. Assuming that in this region the distribution of velocities of the particle is the Maxwell-Boltzmann distribution:

$$f(\mathbf{v})=\frac{m^{3/2}}{(2\pi k_BT)^{3/2}}e^{-\frac{mv^2}{2k_BT}}$$ (2.26)

the collision frequency can be calculated obtaining the formula:

$$\nu=\sqrt{2}nS\overline{v}$$ (2.27)

where $\overline{v}$ is the average of the modulus of the velocities and, in this case, is given by:

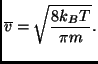$$\overline{v}=\sqrt{\frac{8k_BT}{\pi m}}.$$ (2.28)

In the same way the mean free path is given by

$$\lambda=\frac{1}{\sqrt{2}nS}.$$ (2.29)