Let us consider two point-like particles with masses ![]() and
and ![]() ,
coordinates
,
coordinates
![]() and
and
![]() and velocities
and velocities
![]() and
and
![]() . One can introduce the center of
mass vector
. One can introduce the center of
mass vector
![]() :
:
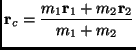 |
(2.1) |
and the relative position vector:
| (2.2) |
Their time derivatives are: the velocity of the center of mass:
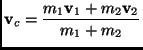 |
(2.3) |
and the relative velocity:
| (2.4) |
The forces between these two particles depends only on their relative position and are of equal magnitude and pointing in opposite directions:
| (2.5) |
This is equivalent to say that the center of mass does not accelerate, i.e.:
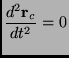 |
(2.6) |
while the relative position obeys to the following equation of motion:
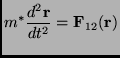 |
(2.7) |
where
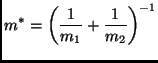 |
(2.8) |
is the reduced mass of the system of two particles. If the collision is elastic an interaction potential can be introduced so that:
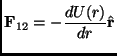 |
(2.9) |
where
![]() is the unit vector along the direction of the
relative position of the two particles. The force vector lies in the
same plane where the relative position vector and relative velocity
vector lie. The evolution of the relative position
is the unit vector along the direction of the
relative position of the two particles. The force vector lies in the
same plane where the relative position vector and relative velocity
vector lie. The evolution of the relative position ![]() is the
evolution of the position of a particle of mass
is the
evolution of the position of a particle of mass ![]() in a central
potential
in a central
potential ![]() . The angular momentum of the relative motion
. The angular momentum of the relative motion
![]() is conserved. This
means that the particle trajectory, during the collision, will be
confined to this plane. In Fig. 2.1 is sketched the
typical binary scattering event when the interacting force is
repulsive (monotonically decreasing potential), in the center of mass
frame.
is conserved. This
means that the particle trajectory, during the collision, will be
confined to this plane. In Fig. 2.1 is sketched the
typical binary scattering event when the interacting force is
repulsive (monotonically decreasing potential), in the center of mass
frame.
![\includegraphics[clip=true,width=12cm,keepaspectratio]{collision.eps}](img322.png) |
In the center of mass frame the elastic scattering has a very simple
picture: the velocities of the particles are
![]() and
and
![]() . The elastic collision
conserves the modulus of the relative velocity
. The elastic collision
conserves the modulus of the relative velocity ![]() and therefore
also the moduli of the velocities of the particles in the center of
mass frame. If one consider the collision event as a black box and
observes the velocities of the particles ``before'' and ``after'' the
interaction (i.e. asymptotically, when the interaction is negligible),
then the velocity vectors are simply rotated of an angle
and therefore
also the moduli of the velocities of the particles in the center of
mass frame. If one consider the collision event as a black box and
observes the velocities of the particles ``before'' and ``after'' the
interaction (i.e. asymptotically, when the interaction is negligible),
then the velocity vectors are simply rotated of an angle ![]() called angle of deflection, which also represents the angle
between asymptotic initial and final directions of the relative
velocity. During the collision the total momentum is conserved (this
happens also for inelastic collisions) but is redistributed between
the two particles, i.e. the variation of the momentum of the particle
called angle of deflection, which also represents the angle
between asymptotic initial and final directions of the relative
velocity. During the collision the total momentum is conserved (this
happens also for inelastic collisions) but is redistributed between
the two particles, i.e. the variation of the momentum of the particle
![]() is
is
![]() where the prime indicates the post-collisional relative
velocity. Obviously
where the prime indicates the post-collisional relative
velocity. Obviously
![]() . Finally, one can
calculate the components of the momentum transfer parallel and
perpendicular to the relative velocity:
. Finally, one can
calculate the components of the momentum transfer parallel and
perpendicular to the relative velocity:
To calculate the angle of deflection ![]() one needs the
exact form of the interaction potential, the asymptotic initial
relative velocity
one needs the
exact form of the interaction potential, the asymptotic initial
relative velocity ![]() (i.e. at a distance such that the
interaction is negligible) and the impact parameter
(i.e. at a distance such that the
interaction is negligible) and the impact parameter ![]() that is
the minimal distance between the trajectories of the particles if
there were no interaction between them:
that is
the minimal distance between the trajectories of the particles if
there were no interaction between them:
where ![]() is the closest distance effectively reached by the two
particles. From Eq. (2.11) it is evident that the angle of
deflection decreases as the initial relative velocity increases.
is the closest distance effectively reached by the two
particles. From Eq. (2.11) it is evident that the angle of
deflection decreases as the initial relative velocity increases.
The case of an inverse power potential is of physical interest:
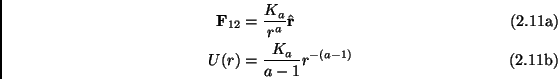 |
with ![]() and
and ![]() positive or negative in order to have
respectively repulsive or attractive forces. In this case
Eq. (2.11) can be explicitly calculated for some specific
values of the power
positive or negative in order to have
respectively repulsive or attractive forces. In this case
Eq. (2.11) can be explicitly calculated for some specific
values of the power ![]() . For example the gravitational or
electrostatic interactions (in 3D) correspond to the case
. For example the gravitational or
electrostatic interactions (in 3D) correspond to the case ![]() for which
for which
![$\displaystyle \chi=2 \arcsin \left[ \frac{1}{\sqrt{1+x_0^2}} \right]$](img339.png) |
(2.13) |
where
![]() . The case
. The case ![]() is even simpler leading to the formula
is even simpler leading to the formula
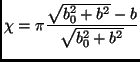 |
(2.14) |
with
![]() . The case
. The case ![]() (in 3D) is of
particular interest because for this special interaction the kinetic
equation (Boltzmann equation, see section 2.2.3) is
very simple. Particles interacting with this potential are called
Maxwell molecules, discussed in more detail in paragraph
2.2.5. The deflection angle for this case is quite
complicated:
(in 3D) is of
particular interest because for this special interaction the kinetic
equation (Boltzmann equation, see section 2.2.3) is
very simple. Particles interacting with this potential are called
Maxwell molecules, discussed in more detail in paragraph
2.2.5. The deflection angle for this case is quite
complicated:
![$\displaystyle \chi=\pi-\int_0^1du\frac{2^{3/2}x_0\sqrt{\sqrt{x_0^4+2}-x_0^2}}{\sqrt{(x_0^4+2)-\left\{x_0^2+u^2\left[\sqrt{x_0^4+2}-x_0^2 \right] \right\}^2}}$](img345.png) |
(2.15) |
with
![]() . For small values of
. For small values of ![]() (i.e. for small impact parameters or small initial relative
velocities) the deflection angle approaches
(i.e. for small impact parameters or small initial relative
velocities) the deflection angle approaches ![]() linearly, i.e.:
linearly, i.e.:
| (2.16) |