The Maxwell molecules

The collisional integral of Boltzmann equation for hard spheres, Eq. (2.76), contains a term $g=\vert\mathbf{V} \cdot \hat{\mathbf{n}}\vert$ which multiplies the probabilities of particles entering or coming out from a collision. In general the collisional integral must contain the differential collision rate $dR/D\Omega$ for particle coming at a certain relative velocity (in modulus $g$ and direction $\hat{\mathbf{n}}$, or equivalently scattering angle $\chi$ centered in the solid angle $d\Omega$), which may be expressed in terms of the scattering cross section $s$ (see for example Eq. (2.20)):

$$\frac{dR}{d\Omega}=gs(g,\chi)P_2(\mathbf{r},\mathbf{r}+\sigma\hat{\mathbf{n}},\mathbf{v}_1,\mathbf{v}_2,t)d\mathbf{v}_2$$ (2.84)

We discussed in paragraph 2.1.2 the fact that the scattering cross section depends strongly on the kind of interaction between the molecules of the gas. For power law repulsive interaction potential $V(r) \sim r^{-(a-1)}$, the scattering angle $\chi$ depends on the relative energy $g^2/2$ and on the impact parameter $b$ only through the combination $(g^2b^{a-1})$ (see for example [59]). This means that there exists a function $\gamma(\chi)$ such that:

$$b=g^{-2/(a-1)}\gamma(\chi)$$ (2.85)

and this means that from relation (2.22) one obtains:

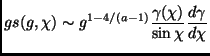$$gs(g,\chi) \sim g^{1-4/(a-1)}\frac{\gamma(\chi)}{\sin \chi}\frac{d\gamma}{d\chi}$$ (2.86)

which holds in $d=3$. The extension to generic dimension of the last equation is:

$$gs(g,\chi) \sim g^{1-2(d-1)/(a-1)}\frac{\gamma^{d-2}}{(\sin \chi)^{d-2}}\frac{d\gamma}{d\chi} \sim g^{1-2(d-1)/(a-1)}\alpha(\cos \chi)$$ (2.87)

Therefore when $a=1+2(d-1)$ (i.e. $a=5$ for $d=3$ and $a=3$ for $d=2$) the collision rate $gs(g,\chi)$ does not depend upon $g$. This property defines the so-called Maxwell molecules [81]. Interaction with $a<1+2(d-1)$ are called soft interactions (e.g. the electrostatic or gravitational interaction). Interactions with $a>1+2(d-1)$ are called hard interactions. Hard spheres ( $a \to \infty$) belongs to this set of interactions, with $gs(g,\chi) \sim g$. It has been also studied the Very Hard Particles model, which is characterized by $gs(g,\chi) \sim g^2$, which is not attainable with an inverse power potential, as it requires an interaction harder than the hard sphere interaction.

The obvious advantage of Maxwell molecules is that the Boltzmann equation greatly simplifies, as $g$ does not appear in the collision integral. A further simplification of the Boltzmann equation came from Krook and Wu [129], who studied the Boltzmann equation of Maxwell molecules with an isotropic scattering cross-section, i.e $\alpha = const$, often called Krook and Wu model. A very large literature exists for linear and non-linear model-Boltzmann equations (for a review see [81]). The importance of the Maxwell molecules model is the possibility of obtaining solutions for it: the general method (extended to other model-Boltzmann equations) is to obtain an expansion in orthogonal polynomial where the expansion coefficients are polynomial moments of the solution distribution function. For Maxwell molecules the moments satisfy a recursive system of differential equations that can be solved sequentially. Given an initial distribution, one can solve the problem if the series expansion converges. Bobylev [32] has shown that if one searches for similarity solutions (i.e. solutions with scaling form $P(\mathbf{v},t) \equiv e^{-\alpha t}F(e^{-\alpha t}\mathbf{v})$), then the solution can be found solving a recursive system of algebraic equation.

The Maxwell molecules model has been subject of study also in the framework of the kinetic theory of granular gases. In section 5.3 we discuss this issue.