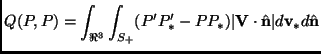 |
(2.73) |
The integral appearing in the right-hand side of Eq. (2.74) is usually called collision integral:
where we have used an intuitive contracted notation (the prime or ![]() must be considered applied to the velocity vector in the argument of
the function
must be considered applied to the velocity vector in the argument of
the function ![]() ). In the collision integral, the position
). In the collision integral, the position
![]() is the same wherever the function
is the same wherever the function ![]() appears, and therefore
it can be considered a parameter of
appears, and therefore
it can be considered a parameter of ![]() .
.
Let us have a look to the integral
which can be transformed in many alternative forms, using its symmetries. In particular one can exchange primed and unprimed quantities, as well as starred and unstarred quantities. With manipulations of this sort, it is immediate to get the following alternative form of Eq. (2.77):
From this equation it comes that if
almost everywhere in velocity space, then the integral of
Eq. (2.78) is zero independent of the
particular function ![]() . Many authors have proved under different
assumptions that the most general solution of Eq. (2.79) is given by
. Many authors have proved under different
assumptions that the most general solution of Eq. (2.79) is given by
Furtherly, if
![]() , from Eq. (2.78) it follows that
, from Eq. (2.78) it follows that
which follows from the elementary inequality
![]() if
if
![]() . This becomes an equality if and only if
. This becomes an equality if and only if ![]() ,
therefore the equality sign holds in Eq. (2.81) if and only
if
,
therefore the equality sign holds in Eq. (2.81) if and only
if
This is equivalent to two important facts:
Equation (2.81) is a fundamental result of the Boltzmann theory (it is often called Boltzmann Inequality) and can be fully appreciated with the following discussion: we rewrite the Boltzmann Equation (2.74) with a simplified notation:
We multiply both sides by
![]() and integrate with respect to
and integrate with respect to
![]() , obtaining a transport equation for the quantity
, obtaining a transport equation for the quantity ![]() :
:
Then Eq. (2.81) states that
![]() and
and ![]() if
and only if
if
and only if ![]() is a Maxwellian. For example, if we look for a space
homogeneous solution of the Boltzmann equation, it happens that
is a Maxwellian. For example, if we look for a space
homogeneous solution of the Boltzmann equation, it happens that
that is the famous H-Theorem. It simply states that there exists a
macroscopic quantity (![]() in this case) that decreases as the gas
evolves in time and eventually goes to zero when (if and only if) the
distribution
in this case) that decreases as the gas
evolves in time and eventually goes to zero when (if and only if) the
distribution ![]() becomes a Maxwellian. When the homogeneity is not
achievable (due to non-homogeneous boundary conditions) rigorous
results are more complicated, but we are still tempted to say
that the Maxwellian represents the local asymptotic equilibrium, with
the spatial dependence carried by the parameters of this distribution
function.
becomes a Maxwellian. When the homogeneity is not
achievable (due to non-homogeneous boundary conditions) rigorous
results are more complicated, but we are still tempted to say
that the Maxwellian represents the local asymptotic equilibrium, with
the spatial dependence carried by the parameters of this distribution
function.
The H-Theorem shows that the Boltzmann equation, apparently obtained
from microscopic reversible principles, has a basic feature of
irreversibility: the trajectories in the phase space that corresponds
to evolutions of the one-particle probability distribution that give
place to an increase of ![]() with time are not solutions of the
Boltzmann equation, even if they are compatible with the given
collision rules, i.e. with the laws of Newtonian mechanics. This
paradox [207,142] is nowadays discussed in the
following way [61]: the assumption of Molecular Chaos
is the source of irreversibility, the choice of factorization of
probability for molecules that go into a collision induces
correlations for the molecules that go out of a collision. If
the velocity of all the molecules would be inverted at a certain time,
the one particle probability distribution would no more satisfy the
Molecular Chaos hypothesis and the Boltzmann equation could not
describe the system. In general ``no kind of irreversibility cam
follow by correct mathematics from the analytical dynamics of a
conservative system'' (Cercignani et al. [61]). The
other paradox often cited as a consequence of the H-Theorem is the
so-called Zermelo's paradox [180,227]: Zermelo noted
that the ``recurrence theorem'' of Poincare [179] is in
contrast with the H-Theorem. The recurrence theorem guarantees that
the molecules of the gas, after a ``recurrence time'', can have
positions and velocities so close to the initial ones that the one
particle distribution would be practically the same, that is if it
decreased initially, then it must have increased ad some later time.
The answer of Boltzmann [35] to this objection is that
the recurrence time is so large that, practically speaking, one would
never observe a significant portion of the recurrence cycle. From a
rigorous point of view, the Boltzmann-Grad limit (
with time are not solutions of the
Boltzmann equation, even if they are compatible with the given
collision rules, i.e. with the laws of Newtonian mechanics. This
paradox [207,142] is nowadays discussed in the
following way [61]: the assumption of Molecular Chaos
is the source of irreversibility, the choice of factorization of
probability for molecules that go into a collision induces
correlations for the molecules that go out of a collision. If
the velocity of all the molecules would be inverted at a certain time,
the one particle probability distribution would no more satisfy the
Molecular Chaos hypothesis and the Boltzmann equation could not
describe the system. In general ``no kind of irreversibility cam
follow by correct mathematics from the analytical dynamics of a
conservative system'' (Cercignani et al. [61]). The
other paradox often cited as a consequence of the H-Theorem is the
so-called Zermelo's paradox [180,227]: Zermelo noted
that the ``recurrence theorem'' of Poincare [179] is in
contrast with the H-Theorem. The recurrence theorem guarantees that
the molecules of the gas, after a ``recurrence time'', can have
positions and velocities so close to the initial ones that the one
particle distribution would be practically the same, that is if it
decreased initially, then it must have increased ad some later time.
The answer of Boltzmann [35] to this objection is that
the recurrence time is so large that, practically speaking, one would
never observe a significant portion of the recurrence cycle. From a
rigorous point of view, the Boltzmann-Grad limit (
![]() )
guarantees that the Poincare recurrence theorem cannot be applied, as
it works for a compact set: the recurrence time is expected to go to
infinity.
)
guarantees that the Poincare recurrence theorem cannot be applied, as
it works for a compact set: the recurrence time is expected to go to
infinity.
Solutions of the Boltzmann equation in the form of a Maxwellian
distribution with space dependent parameters (in the case of a steady
solution, i.e.
![]() ) or space-time dependent
parameters (in the dynamic case) can be found. The equations that
govern the space-time evolution of the parameters of the Maxwellian
are the Euler equations (see section 2.3.4). The Euler equations
are based on a very important assumption, usually called hydrodynamical limit. If we solve the Boltzmann equation in a box of
side
) or space-time dependent
parameters (in the dynamic case) can be found. The equations that
govern the space-time evolution of the parameters of the Maxwellian
are the Euler equations (see section 2.3.4). The Euler equations
are based on a very important assumption, usually called hydrodynamical limit. If we solve the Boltzmann equation in a box of
side
![]() we obtain a solution
we obtain a solution
![]() . If we enlarge the box
(i.e.
. If we enlarge the box
(i.e. ![]() is reduced toward zero), while keeping the total
number of particles proportional to the volume of the box, then the
solution
is reduced toward zero), while keeping the total
number of particles proportional to the volume of the box, then the
solution
![]() will assume a
will assume a ![]() -dependent form. In
order to regard the linear size of the box as being of order unity,
we may rescale the space-time variables:
-dependent form. In
order to regard the linear size of the box as being of order unity,
we may rescale the space-time variables:
![]() ,
,
![]() ,
,
![]() .
With this new variables, the mean free path (that is of order unity on
the
.
With this new variables, the mean free path (that is of order unity on
the
![]() scale) becomes of order
scale) becomes of order ![]() . The distribution
. The distribution
![]() solves a different Boltzmann equation in the new variables:
solves a different Boltzmann equation in the new variables:
 |
(2.83) |
As the term ![]() is of order unity (Boltzmann-Grad limit, taken
before) we must require that
is of order unity (Boltzmann-Grad limit, taken
before) we must require that
![]() is of order
is of order
![]() so that we can take the limit
so that we can take the limit
![]() . In other words,
the hydrodynamical limit is a change of the level of description from
the microscopic to the macroscopic one: at the macroscopic
level the average number of collisions (
. In other words,
the hydrodynamical limit is a change of the level of description from
the microscopic to the macroscopic one: at the macroscopic
level the average number of collisions (
![]() )
diverges and therefore we ask that the average effect of a single
collision (given by
)
diverges and therefore we ask that the average effect of a single
collision (given by ![]() ) is very small. Then taking the hydrodynamical
limit, we expect that
) is very small. Then taking the hydrodynamical
limit, we expect that ![]() is close to a Maxwellian (as it is the
only solution of the equation
is close to a Maxwellian (as it is the
only solution of the equation ![]() ). In other words, the possibility
of a macroscopic description is strictly tied to the possibility of a
separation of scales: at the microscopic scale the phenomena are
very rapid, i.e. the distribution function rapidly ``thermalizes''
coming toward the Maxwellian, while at the macroscopic scale the
evolution of the gas is viewed as a slow evolution of the space-time
dependent parameters of the Maxwellian, given by the hydrodynamic
equations. If the ``thermalization'' stated above is so rapid
that the distribution function
). In other words, the possibility
of a macroscopic description is strictly tied to the possibility of a
separation of scales: at the microscopic scale the phenomena are
very rapid, i.e. the distribution function rapidly ``thermalizes''
coming toward the Maxwellian, while at the macroscopic scale the
evolution of the gas is viewed as a slow evolution of the space-time
dependent parameters of the Maxwellian, given by the hydrodynamic
equations. If the ``thermalization'' stated above is so rapid
that the distribution function ![]() is always a Maxwellian, at
any instant
is always a Maxwellian, at
any instant ![]() , then the fluid is considered ideal and it is
governed by the Euler equations (see paragraph
2.3.4). Otherwise, the evolution toward the Maxwellian is
somewhat a dissipative process (in the sense of its irreversibility):
it is the aim of the kinetic theory of transport to describe its
behavior. Assumptions on the ``closeness'' to the Maxwellian gives, in
last analysis, the well known Navier-Stokes equations for non-ideal
fluids (see paragraph 2.3.7).
, then the fluid is considered ideal and it is
governed by the Euler equations (see paragraph
2.3.4). Otherwise, the evolution toward the Maxwellian is
somewhat a dissipative process (in the sense of its irreversibility):
it is the aim of the kinetic theory of transport to describe its
behavior. Assumptions on the ``closeness'' to the Maxwellian gives, in
last analysis, the well known Navier-Stokes equations for non-ideal
fluids (see paragraph 2.3.7).