The Navier-Stokes approximation

The most complicated of the transport equations presented above is that for the general heat flow $\mathcal{Q}$ . This set of

scalar quantities are tied to the fourth order corrections in the Chapman-Enskog expansion (see (2.135)). In most physical problems it is usually sufficient to know the evolution of the contracted quantity $\mathbf{q}$ defined in Eq. (2.119), which represents the transport of the total (modulus) random energy of the particles due to the random motion of the molecules (we lose accuracy on the transport of single random velocity components). Therefore we make the assumption:

$\displaystyle Q_{ijk}=\frac{2}{3}(\delta_{ij}q_k+\delta_{ik}q_j+\delta_{jk}q_i),$

(2.134)

With this further assumption it is more easy to perform the BGK calculation of the collision terms that appear in the stress and heat tensor equations (2.138). Bypassing the details the final formula are:

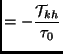$\displaystyle \frac{\delta \mathcal{T}_{kh}}{\delta t}$	$\displaystyle =-\frac{\mathcal{T}_{kh}}{\tau_0}$	(2.135)
$\displaystyle \frac{\delta q_k}{\delta t}$	$\displaystyle =-\frac{q_k}{\tau_0}.$	(2.136)

This last result is very important if inserted in equations (2.138). In fact it must be noted that the second and third order expansion coefficients (ultimately tied to $\mathcal{T}$ and $\mathbf{q}$ ) are usually negligibly small, except when they are multiplied by very large factors, in this case $1/\tau_0$ . The Chapman-Enskog method can only be applied to gases which are not far from equilibrium: this means that very frequent collisions must nearly absorb all deviations from equilibrium. In other words the relaxation time $\tau_0$ must be extremely short. Based on this argument, we can neglect all terms containing the stress tensor and the heat flow vector, except the ones which are multiplied by $1/\tau_0$ , obtaining (for the case $\mathbf{a}=0$ ):

$\begin{subequations}\begin{align}\mathcal{T}_{kl} &=\tau_0p_0\left(\frac{\partia... ...{k_B}{m}\tau_0p_0\frac{\partial T_0}{\partial r_k} \end{align}\end{subequations}$

which is the familiar linear relation between the flows and the gradients: momentum flow (non-diagonal) is proportional to the velocity gradient, heat flow is proportional to temperature gradient. Having recognized that, the hydrodynamic transport coefficients (viscosity and heat conductivity) can be expressed:

$\begin{subequations}\begin{align}\eta &=\tau_0p_0 \ \kappa &=\frac{5}{2}\frac{k_B}{m}\tau_0p_0 \end{align}\end{subequations}$

that are equivalent (with slight differences in the numerical constants) with the mean free path calculations discussed in paragraph 2.1.4.

$\begin{subequations}\begin{gather}\frac{\partial(mn_0)}{\partial t}+\frac{\parti... ...r_i} \right)\frac{\partial u_{0,k}}{\partial r_l} \end{gather}\end{subequations}$

These equations represent the most simple form of transport equations for a gas that is not in strict local thermodynamic equilibrium (which instead is described by Euler equations (2.123)). The deviation from equilibrium is slight but important, as irreversible (dissipative) processes emerge from it: these are taken into account by the linear transport coefficients (viscosity and heat conductivity) which represent the tendency of the gas to relax toward the Maxwellian equilibrium.