The Chapman-Enskog closure

In elastic gases not so dense but not so rarefied the deviation from the Maxwell-Boltzmann equilibrium distribution is small and it can be treated as a perturbation. This is the main motivation of Chapman-Enskog method [62] to obtain transport equations more general than the Euler equations. The local distribution function is expanded around a reference unperturbed distribution, which is assumed to be a Maxwell-Boltzmann distribution with parameters depending on time and space: the local number density $n_0(t,\mathbf{r})$, local temperature $T_0(t,\mathbf{r})$ and local flow velocity vector $\mathbf{u}_0(t,\mathbf{r})$:

$$P_0(t,\mathbf{r},\mathbf{c})=n_0(t,\mathbf{r}) \left( \frac{m}{2\... ...^{3/2} \exp \left( - \frac{m(c_1^2+c_2^2+c_3^2)}{2k_BT_0(t,\mathbf{r})} \right)$$ (2.119)

with $\mathbf{c}=\mathbf{v}-\mathbf{u}_0$.

The series expansion around this reference distribution reads:

$$P(t,\mathbf{r},\mathbf{c})=P_0(t,\mathbf{r},\mathbf{c}) \left\{ 1... ...,\mathbf{r})c_i c_j + \mathcal{D}_{ijk}(t,\mathbf{r})c_i c_j c_k + ... \right\}$$ (2.120)

where the expansion coefficient matrices are symmetric for the interchange of indexes.

The normalization conditions implies that

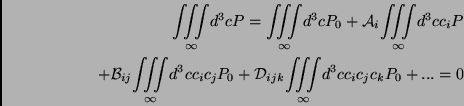$$\begin{split}\underset{\infty}{\iiint}d^3cP=\underset{\infty}... ...k}\underset{\infty}{\iiint}d^3cc_ic_jc_kP_0 + ...=0 \end{split}$$ (2.121)

which, noting that the averages of odds momenta of $\mathbf{c}$ are zero, becomes:

$$\mathcal{B}_{ii}+ +...=0.$$ (2.122)

Using the fact that the average random velocity must be identically zero, another condition is obtained for the expansion coefficients:

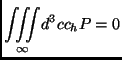$$\underset{\infty}{\iiint}d^3cc_hP=0$$ (2.123)

which (as the odd order vanish) becomes:

$$\mathcal{A}_i \langle c_h c_i \rangle_0 + \mathcal{D}_{ijk} \langle c_h c_i c_j c_k \rangle_0 + ...=0.$$ (2.124)

where $\langle \rangle_0$ are the averages weighted by the Maxwell-Boltzmann distribution $P_0$.

Assuming that the higher order terms of the expansion represent a decreasing series of perturbations, one can truncate the expansion to some low order. The zero order truncation gives, of course, a trivial approximation. First and second order truncations cannot be obtained as the condition of Eq. (2.131) requires the presence of at least two terms of odd orders (the first and the third). Therefore the lowest non-trivial possible expansion is the third order one, for which the above conditions (after having calculated the $\langle \rangle_0$ averages) read:

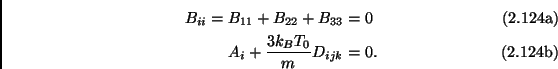The zero order expansion requires $5$ independent parameters (that in transport equations become transported fields): density $n_0$, momentum $m\mathbf{u}_0$ and temperature $T_0$. The third order expansion requires $5+3+6+10=24$ parameters (it must be remembered that the coefficient matrices are symmetric) but the last couple of conditions (which are four) reduce the number of independent parameters to $20$.

The Chapman-Enskog expansion is usually truncated to the first non-trivial order, that is the third, for which the first velocity moments read (with also the use of the above conditions):

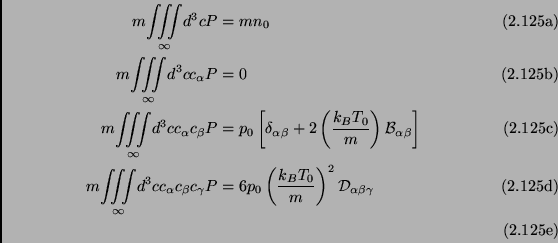with $p_0=n_0k_BT_0$. From them one can immediately identify the macroscopic physical quantities introduced in the first paragraph of this section, mainly the stress and heat flow tensors:

$$\mathcal{T}_{\alpha \beta}=-2p_0 \left( \frac{k_BT_0}{m}\mathcal{B}_{\alpha \beta} \right)$$ (2.127)

$$\mathcal{Q}_{\alpha \beta \gamma}=6p_0 \left( \frac{k_BT_0}{m} \right)^2 \mathcal{D}_{\alpha \beta \gamma}$$ (2.128)

coming to the conclusion that the third order Chapman-Enskog expansion of the phase space distribution function reads:

$$P=P_0 \left[ 1 - \frac{mn_0}{2p_0^2}\mathcal{T}_{ij}c_ic_j+\frac{... ...eft(\mathcal{Q}_{ijk}c_jc_k-\frac{3p_0}{mn_0}\mathcal{Q}_{ijj}\right)c_i\right]$$ (2.129)

With the third order truncation, it happens that the fourth moment $\mathcal{R}$ given in Eq. (2.120) is only a function of the parameters of the Maxwellian reference state $P_0$ (precisely only of $n_0$ and $p_0$) and of the second order tensor $\mathcal{B}$, or equivalently of the stress tensor $\mathcal{T}$. Again we have $20$ free parameters: the $5$ parameters of the Maxwellian $n_0$; $\mathbf{u}_0$ and $p_0$, the $5$ elements of the traceless symmetric stress tensor $\mathcal{T}$, and the $10$ elements of the symmetric heat flux matrix $\mathcal{Q}$. And again we obtain (as with the Grad closure method) $1+3+6+10=20$ transport equations, which we divide in two groups: the equations for the $5$ parameters of the reference Maxwellian,

and the $5+10=15$ equations for the stress and heat tensors:

Keeping in mind the decomposition of the pressure tensor (2.117) it can be immediately seen that the first two equations in (2.137) (continuity and motion equations) are identical to that obtained by Grad. Moreover the last of (2.137) joined with the first of (2.138) are equivalent to (2.122c) which is the third equation of Grad's closure. The only difference between Grad and Chapman-Enskog method is in the equation for the heat flow tensor (Eqs. (2.138b) and (2.125)) and it appears to be a fourth order difference as it comes only from the appearance in Eq. (2.125) of terms containing $\mathcal{T}^2$ (which are related to the second order coefficients of the expansion $\mathcal{B}$, see Eq. (2.134)). We can conclude that the Chapman-Enskog expansion method and the Grad closure method are equivalent to third order accuracy.

Finally we must observe that the derivation of the transport equations is somewhat not complete, as (in both Grad and Chapman-Enskog formulas) the collision terms $\frac{\delta}{\delta t}$ remain unexpressed. The only non-trivial collision terms are that for the stress and heat flow tensors (non-diagonal second order moments and third order moments of the Boltzmann collision terms), as the mass, velocity and energy are conserved during collisions, so that:

The collision terms for the last two equations (2.138) can be approximated with the well known BGK approximation, due to Bhatnagar, Gross and Krook [27], also known as relaxation time approximation. In a few word it states that

$$\frac{\delta P}{\delta t}=-\frac{P-P_0}{\tau_0}.$$ (2.133)

This means that as a consequence of the randomizing effect of collisions the distribution function tends to the equilibrium Maxwellian in an exponential way with a characteristic relaxation time $\tau_0$ which remains a free parameter of the theory, to be calculated with other considerations. If one has a truncated expansion of $P$ around the Maxwellian $P_0$, than Eq. (2.140) yields an expression for the collisional variations of all the needed velocity moments.