The BBGKY hierarchy

We define the reduced (marginal) probability densities $P_s$ as

$$P_s(\mathbf{r}_1,\mathbf{v}_1,\mathbf{r}_2,\mathbf{v}_2,...,\math... ...v}_2,...,\mathbf{r}_N,\mathbf{v}_N,t) \prod_{j=s+1}^Nd\mathbf{r}_jd\mathbf{v}_j$$ (2.62)

In order to derive an evolution equation for $P_s$ the first step is to integrate Eq. (2.55) with respect to the variables $\mathbf{r}_j$ and $\mathbf{v}_j$ ( $s+1\leq j\leq N)$ over $\Omega^{N-s} \times \Re^{3(N-s)}$, obtaining:

$$\frac{\partial P_s}{\partial t}+\sum_{i=1}^s \int_{\Lambda_s} \ma... ...partial P}{\partial \mathbf{r}_k} \prod_{j=s+1}^N d\mathbf{r}_j d\mathbf{v}_j=0$$ (2.63)

where the integration space $\Lambda_s$ extends to the entire $\Re^{3(N-s)}$ for the velocity variables, while it extends to $\Omega^{N-s}$ deprived of the spheres $\vert\mathbf{r}_i-\mathbf{r}_j\vert<\sigma$ ( $i=1,...,N,i\neq j$) with respect to the position variables.

The typical term in the first sum contains the integral of a derivative with respect to a variable $\mathbf{r}_i$ over which one does not integrate, but in the exchange of order between integration and derivation one must take into account the domain boundaries which depend on $\mathbf{r}_i$, writing:

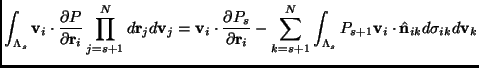$$\int_{\Lambda_s} \mathbf{v}_i \cdot \frac{\partial P}{\partial \m... ...bda_s} P_{s+1}\mathbf{v}_i \cdot \hat{\mathbf{n}}_{ik}d\sigma_{ik}d\mathbf{v}_k$$ (2.64)

where $\hat{\mathbf{n}}_{ik}$ is the outer normal to the sphere $\vert\mathbf{r}_i-\mathbf{r}_k\vert=\sigma$, $d\sigma_{ik}$ is the surface element on the same sphere and $P_{s+1}$ has $k$ as its $(s+1)-th$ index.

The typical term in the second sum in Eq. (2.64) can be immediately integrated by means of the Gauss theorem, since it involves the integration of a derivative taken with respect to one of the integration variables (and assuming that the boundary of $\Omega$ is a specular reflecting wall or a periodical boundary condition):

$$\begin{multline} \int_{\Lambda_s} \mathbf{v}_k \cdot \frac{\partial P}{\partial ... ...thbf{n}}_{ik}d\sigma_{ik}d\mathbf{v}_kd\mathbf{r}_i d\mathbf{v}_i \end{multline}$$

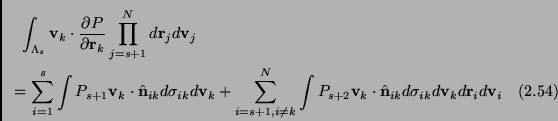
The last term in the above equation, when summed over $s+1 \leq k \leq N$ vanishes: this fact directly stems from the equivalence (2.55b) (we do not enter in the few steps of this simple proof). Moreover, in both above equations the integral containing the term $P_{s+1}$ is the same no matter what the value of the dummy index $k$ is, so that we can drop the index and write $\mathbf{r}_*,\mathbf{v}_*$ instead of $\mathbf{r}_k,\mathbf{v}_k$.

As a matter of fact, Eq. (2.64) finally reads:

$$\frac{\partial P_s}{\partial t} + \sum_{i=1}^s \mathbf{v}_i \cdot... ...}^s \int P_{s+1} \mathbf{V}_i \cdot \hat{\mathbf{n}}_i d\sigma_i d \mathbf{v}_*$$ (2.65)

where $\mathbf{V}_i=\mathbf{v}_i-\mathbf{v}_*$, $\hat{\mathbf{n}}_i=(\mathbf{r}_i-\mathbf{r}_*)/\sigma$ and the arguments of $P_{s+1}$ are $(\mathbf{r}_1,\mathbf{v}_1,\mathbf{r}_2,\mathbf{v}_2,...,\mathbf{r}_s,\mathbf{v}_s,\mathbf{r}_*,\mathbf{v}_*,t)$. Integrations in Eq. (2.67) are performed over the 1-particle velocity space $\Re^3$ and over the sphere $S^i$ (given by the condition $\vert\mathbf{r}_i-\mathbf{r}_*\vert=\sigma$) with surface elements $d\sigma_i$.

Eq. (2.67) states that the evolution of the reduced probability density $P_s$ is governed by the free evolution operator of the $s$-particles dynamics, which appears in the left hand side, with corrections due to the effect of the interaction with the remaining $(N-s)$ particle. The effect of this interaction is described by the right-hand side of this equation.

Usually Eq. (2.67) is written in a different form, obtained using some symmetries of the problem. In particular one can separate the sphere $S^i$ of integration in the right-hand side, in the two hemispheres $S_+^i$ and $S_-^i$ defined respectively by $\mathbf{V_i} \cdot \hat{\mathbf{n}}_i >0$ and $\mathbf{V_i} \cdot \hat{\mathbf{n}}_i <0$ (considering also that $d\sigma_i=\sigma^2d\hat{\mathbf{n}}_i$):

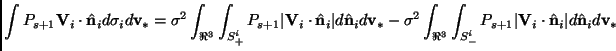$$\int P_{s+1} \mathbf{V}_i \cdot \hat{\mathbf{n}}_i d\sigma_i d \m... ...rt\mathbf{V}_i \cdot \hat{\mathbf{n}}_i\vert d\hat{\mathbf{n}}_i d \mathbf{v}_*$$ (2.66)

and observe that in the $S_+^i$ integration are included all phase space points such that particle $i$ and particle $*$ (the $(s+1)-th$ generic particle) are coming out from a collision: this means that on the sphere $S_+^i$ we can write the substitution

$$\begin{multline} P_{s+1}(\mathbf{r}_1,\mathbf{v}_1,...,\mathbf{r}_i,\mathbf{v}_i... ...{v}_*+\hat{\mathbf{n}}_i(\hat{\mathbf{n}}_i \cdot \mathbf{V}_i)). \end{multline}$$

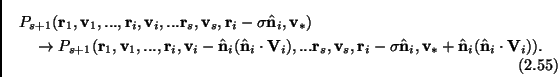
Moreover we can make the change of variable in the second integral (that on the sphere $S_-^i$) $\hat{\mathbf{n}}_i \to -\hat{\mathbf{n}}_i$ which only changes the integration range $S_-^i \to S_+^i$. Finally, replacing $\hat{\mathbf{n}}_i$ with simply $\hat{\mathbf{n}}$ (and therefore $S_+^i \to S_+$) we have:

$$\frac{\partial P_s}{\partial t} + \sum_{i=1}^s \mathbf{v}_i \cdot... ... \vert\mathbf{V}_i \cdot \hat{\mathbf{n}}\vert d\hat{\mathbf{n}} d \mathbf{v}_*$$ (2.67)

where we have defined

$$P_{s+1}'=P_{s+1}(\mathbf{r}_1,\mathbf{v}_1,...,\mathbf{r}_i,\math... ...{n}}_i ,\mathbf{v}_*+\hat{\mathbf{n}}_i(\hat{\mathbf{n}}_i \cdot \mathbf{V}_i))$$ (2.68)

The system of equations (2.70) is usually called the BBGKY hierarchy for the hard sphere gas [60,61].