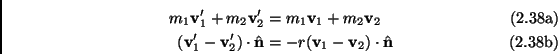 |
Granular particles collide dissipating relative kinetic energy. This is due to the macroscopic nature of the grains which leads to the presence of internal degrees of freedom. During the interaction, irreversible processes happen inside the grain and energy is dissipated in form of heat. All these processes conserve momentum, so that the velocity of the center of mass of the two grains is not modified.
Many modelizations of the binary inelastic collision have been proposed (soft spheres [221,220,52,63,107,146] as well as hard spheres models [53,112,96,159]): this is usually a difficult problem relatively to the information that can be gained from. Simplification often pays more, as very idealized models lead to interesting and physically meaningful results. The most used model in granular gas literature is also the most simple one, that is the inelastic smooth hard spheres gas with the fixed restitution coefficient rule given by the following prescriptions:
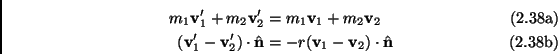 |
where, as usual, the primes denote the postcollisional velocities,
![]() is the unity vector in the direction joining the
centers of the grains, and
is the unity vector in the direction joining the
centers of the grains, and
![]() . In this model the
collisions happen at contact and are instantaneous. When
. In this model the
collisions happen at contact and are instantaneous. When ![]() the gas
is elastic and the rule coincides with the collision description for
hard spheres given in the paragraph 2.1.3. When
the gas
is elastic and the rule coincides with the collision description for
hard spheres given in the paragraph 2.1.3. When ![]() the gas is
perfectly inelastic, that is the particles exit from the collision
with no relative velocity in the
the gas is
perfectly inelastic, that is the particles exit from the collision
with no relative velocity in the
![]() direction.
direction.
As a matter of fact, the transformation that gives the (primed) postcollisional velocities from the precollisional velocities of the two colliding particles is
Sometimes it may be useful to have the reverse transformation that give precollisional velocities from postcollisional ones, with the primes exchanged:
As it can be seen, the inverse transformation is equivalent to a
change of the restitution coefficient ![]() . Obviously in the
case of a perfectly inelastic gas (
. Obviously in the
case of a perfectly inelastic gas (![]() ) there is no inverse
transformation. We also note that in 1D and when
) there is no inverse
transformation. We also note that in 1D and when ![]() Eqs. (2.41) become:
Eqs. (2.41) become:
which coincide to an exact exchange of velocities in the elastic
(![]() ) case, and in a sticky collision in the perfectly inelastic
(
) case, and in a sticky collision in the perfectly inelastic
(![]() ) case. In dimensions higher than one the
) case. In dimensions higher than one the ![]() case is
very different from the so-called sticky gas, which is defined
as a gas of hard spheres that in a collision become stuck together. In
one dimension, instead, the
case is
very different from the so-called sticky gas, which is defined
as a gas of hard spheres that in a collision become stuck together. In
one dimension, instead, the ![]() case may be considered
equivalent to a sticky gas but a further prescription of ``stickiness''
must be given in order to consider collisions among more than two
particles.
case may be considered
equivalent to a sticky gas but a further prescription of ``stickiness''
must be given in order to consider collisions among more than two
particles.
Variants of this models have been largely used in the literature. The
importance of tangential frictional forces acting on the grains at
contact may be studied taking into account the rotational degree of
freedom of the particles, i.e. adding a variable
![]() to each grain. The most simplified model which
takes into account the rotational degree of freedom of particles is
the rough hard spheres gas
( [120,151,150,97,156,115,148]). In
this model the postcollisional translational and angular velocities
are given by the following equations (where the bottom signs in
to each grain. The most simplified model which
takes into account the rotational degree of freedom of particles is
the rough hard spheres gas
( [120,151,150,97,156,115,148]). In
this model the postcollisional translational and angular velocities
are given by the following equations (where the bottom signs in ![]() are to be considered for particle
are to be considered for particle ![]() ):
):
where ![]() is the dimensionless moment of inertia defined by
is the dimensionless moment of inertia defined by
![]() (with
(with ![]() the moment of inertia of the hard object),
e.g.
the moment of inertia of the hard object),
e.g. ![]() for disks and
for disks and ![]() for spheres;
for spheres;
![]() is the normal relative velocity component,
is the normal relative velocity component,
![]() is the
tangential velocity component due to translational motion, while
is the
tangential velocity component due to translational motion, while
![]() is the
tangential velocity component due to particle rotation. In
Eqs. (2.44) the tangential restitution coefficient
is the
tangential velocity component due to particle rotation. In
Eqs. (2.44) the tangential restitution coefficient
![]() appears: it may take any value between
appears: it may take any value between ![]() and
and ![]() . When
. When
![]() tangential effects disappear, i.e. rotation is not affected
by collision (rough spheres become smooth spheres). When
tangential effects disappear, i.e. rotation is not affected
by collision (rough spheres become smooth spheres). When ![]() the particles are said to have perfectly rough surface. It can be
easily seen that (when
the particles are said to have perfectly rough surface. It can be
easily seen that (when ![]() ) energy is conserved for
) energy is conserved for
![]() .
.
Moreover, a new class of models for collisions has been recently
introduced, justified by a deeper analysis of the collision
process. In these models the restitution coefficient ![]() (or the
coefficients
(or the
coefficients ![]() and
and ![]() in the more detailed description given
above) depends on the relative velocity of the colliding particles. In
particular it has been seen that the collision tends to become more
and more elastic as the relative velocity tends to zero. This refined
prescription, referred to as 'viscoelastic'
model [108,44], has relevance (usually
quantitative rather than qualitative) in different issues of the
statistical mechanics of granular gases. An important kinetic
instability of the cooling (and sometimes driven) granular gases is
the so-called inelastic collapse [157,159], i.e. a divergence of the local
collision rate due to the presence of a few particles trapped very
close to each other: simulations of the gas with the viscoelastic
model have shown that this instability is removed, suggesting that it
is an artifact of the fixed restitution coefficient idealization.
in the more detailed description given
above) depends on the relative velocity of the colliding particles. In
particular it has been seen that the collision tends to become more
and more elastic as the relative velocity tends to zero. This refined
prescription, referred to as 'viscoelastic'
model [108,44], has relevance (usually
quantitative rather than qualitative) in different issues of the
statistical mechanics of granular gases. An important kinetic
instability of the cooling (and sometimes driven) granular gases is
the so-called inelastic collapse [157,159], i.e. a divergence of the local
collision rate due to the presence of a few particles trapped very
close to each other: simulations of the gas with the viscoelastic
model have shown that this instability is removed, suggesting that it
is an artifact of the fixed restitution coefficient idealization.
Here we give an expression of the leading term for the velocity
dependence of the normal restitution coefficient ![]() in the
viscoelastic model (the viscoelastic theory may be applied to give
also a velocity dependent expressions for the tangential restitution
coefficient):
in the
viscoelastic model (the viscoelastic theory may be applied to give
also a velocity dependent expressions for the tangential restitution
coefficient):
where ![]() depends on the physical properties of the spheres (mass,
density, radius, Young modulus, viscosity).
depends on the physical properties of the spheres (mass,
density, radius, Young modulus, viscosity).