The energy sink

In the inelastic hard spheres model that we consider (see Eq. (2.41)), the total energy change in a collision between two particles with relative velocity $\mathbf{V}_{12}$ is $\Delta E=-(\mathbf{V}_{12} \cdot \hat{\mathbf{n}})^2(1-r^2)m/4$. It follows that in Eqs. (2.122c) the collisional term for the transport of pressure does not vanish (as in (2.139)). in particular it is straightforward to obtain the expression for the collisional change of the trace of the matrix $m<v_i v_j>/2$, i.e. the kinetic energy:

$$\int d\mathbf{v} \frac{1}{2}mv^2 Q_r(P,P)=-(1-r^2)\omega_c(P,P)$$ (2.144)

where

$$\omega_c(P,P)=\frac{m\pi\sigma^2}{16}\int d\mathbf{v}_1d\mathbf{v... ..._1-\mathbf{v}_2\vert^3P(\mathbf{r},\mathbf{v}_1,t)P(\mathbf{r},\mathbf{v}_2,t).$$ (2.145)

Recalling the composition (see Eqs. (2.115)-(2.117) in the isotropic term)

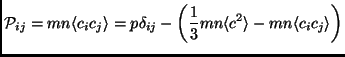$$\mathcal{P}_{ij}=mn \langle c_ic_j \rangle=p\delta_{ij}-\left(\frac{1}{3} mn \langle c^2 \rangle - mn \langle c_i c_j \rangle \right)$$ (2.146)

that defines the stress tensor $\mathcal{T}_{ij}=(mn/3) \langle c^2 \rangle - mn \langle c_i c_j \rangle$ (which in the Chapman-Enskog expansions is seen to be related to the second order term, while the scalar pressure $p$ is of order zero), and also the assumption (2.141) that neglects the differences between the generalized heat flow tensor $\mathcal{Q}$ and the classical heat flow vector $\mathbf{q}$, we can obtain an equation for the evolution of the (zero order) temperature field $T(\mathbf{r},t)$:

$$\frac{\partial T}{\partial t}+u_i\frac{\partial T}{\partial r_i}+... ...frac{\partial q_i}{\partial r_i} \right)+(1-r^2)\frac{2}{3nk_B}\omega_c(P,P)=0.$$ (2.147)

This equation, if compared to Eq. (2.122c) (with $p=nk_BT$), presents a very important difference, that is the presence of the last term in the left-hand side. This term is usually called the energy sink, as it yields the energy dissipation due to inelastic collisions. When $r=1$ (elastic collisions) this term vanishes and the Maxwell equation for the energy transport is recovered.

Mean field considerations can be applied to have rough estimates of the energy sink:

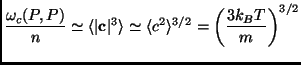$$\frac{\omega_c(P,P)}{n} \simeq \langle \vert\mathbf{c}\vert^3 \rangle \simeq \langle c^2 \rangle^{3/2} = \left( \frac{3k_BT}{m}\right)^{3/2}$$ (2.148)

consequently the energy sink can be written as

$$(1-r^2)\frac{2}{3nk_B}\omega_c(P,P)=2(1-r^2)(3k_B)^{1/2}\left(\frac{T}{m}\right)^{3/2}$$ (2.149)

This mean field estimate assumes that the average of the squared relative velocity at collision is equal to the global average, and that the fractional powers of $\mathbf{c}$ can go in and out of this average. This is the case when the granular gas is homogeneous, i.e. no correlations (in position and velocity) exist between particles. We will show in the following chapters that this situation is far from obvious in real situations. Nevertheless an important result can be obtained by means of Eq. (2.154) with the formula (2.156): in the absence of macroscopic flows Eq. (2.154) reads:

$$\frac{\partial T}{\partial t}=-C_{Haff}T^{3/2}$$ (2.150)

with $C_{Haff}=2(1-r^2)(3k_B)^{1/2}/m^{3/2}$. The fact that the cooling rate (i.e. the temporal derivative of the temperature) is proportional to $T^{3/2}$ when correlations are absent can alternatively be understood with a simple consideration: the reduction of a velocity fluctuation due to an inelastic collision is proportional to the square of the fluctuation itself ($\sim T$), while the total number (per unit time) of collisions is proportional to the total scattering cross section multiplied by the mean velocity fluctuation ( $\sim n\sigma^2\sqrt{T}$); this consideration results in the $T^{3/2}$ cooling rate. The solution of Eq. (2.157) yields the expression for granular temperature (which in this case is equal everywhere in the gas) decay [103]:

$$T(t)=\frac{T_0}{(1+\beta t)^2}$$ (2.151)

that is the widely known as ``Haff law'' for the homogeneous cooling, with $\beta$ easily calculated from Eq. (2.157).