Very recently a complete kinetic theory for granular gases has been proposed [42,41,210,39]. The importance of this effort is in the possibility of the detailed evaluation of validity of the different truncations in the Chapman-Enskog expansion. Moreover this kinetic theory allows a better study of the linearization around a particular state (the so-called ``Homogeneous Cooling State, HCS for further references) and therefore a complete derivation of a linear stability analysis. This is of capital importance to understand many of the results in Chapter V of this work.
The equations obtained by Brey et al. [39] are the following, for dimensions ![]() or
or ![]() :
:
where
![]() is the cooling rate, while the pressure
tensor and heat flux vector are decomposed and linearized in the
following way:
is the cooling rate, while the pressure
tensor and heat flux vector are decomposed and linearized in the
following way:
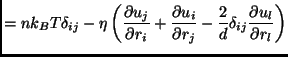 |
(2.154) | |
 |
(2.155) |
with ![]() the shear viscosity,
the shear viscosity, ![]() the thermal conductivity and
the thermal conductivity and
![]() a new transport coefficient which has non analogue in elastic
gases, coupling the density gradient to the heat flux. The exact
expressions for the transport coefficient and for the cooling rate as
functions of the restitution coefficient
a new transport coefficient which has non analogue in elastic
gases, coupling the density gradient to the heat flux. The exact
expressions for the transport coefficient and for the cooling rate as
functions of the restitution coefficient ![]() can be found in the
literature [39,43]. Here we note that - for consistency
with the truncation of the transport fluxes up to the first order in
the gradients, which gives contribution to the hydrodynamic equations,
up to the second order in the gradients - the cooling rate
can be found in the
literature [39,43]. Here we note that - for consistency
with the truncation of the transport fluxes up to the first order in
the gradients, which gives contribution to the hydrodynamic equations,
up to the second order in the gradients - the cooling rate ![]() must be calculated with an expansion truncated up to the second order
(Burnett order). It has been proved that this second order
contribution can be neglected in most situations.
must be calculated with an expansion truncated up to the second order
(Burnett order). It has been proved that this second order
contribution can be neglected in most situations.
The importance of the novel transport coefficient ![]() (not present
in previous formulation of granular hydrodynamics) has been studied by
Soto et al. [203]: they have measured, in a numerical
simulation, the heat flux in a 2D granular gas kept between two walls
at different temperatures, in the presence of gravity, and have
observed that this flux is not zero at the minimum of the temperature
profile (where the gradient of temperature is zero); it depends upon
the gradient of the density and its proportionality coefficient (
(not present
in previous formulation of granular hydrodynamics) has been studied by
Soto et al. [203]: they have measured, in a numerical
simulation, the heat flux in a 2D granular gas kept between two walls
at different temperatures, in the presence of gravity, and have
observed that this flux is not zero at the minimum of the temperature
profile (where the gradient of temperature is zero); it depends upon
the gradient of the density and its proportionality coefficient (![]() in the above equations) depends upon
in the above equations) depends upon ![]() .
.
Brey et al. have also considered the linearization of Eqs. (2.160) around the Homogeneous Cooling State, that is the solution with no spatial gradients:
where ![]() is the solution of the Eq. (2.157) with
is the solution of the Eq. (2.157) with
![]() , where
, where ![]() is a numerical
coefficient (depending upon
is a numerical
coefficient (depending upon ![]() ) and
) and
![]() is the
value of shear viscosity for elastic molecular gases (both this
coefficients can be found in [39]).
is the
value of shear viscosity for elastic molecular gases (both this
coefficients can be found in [39]).
The analysis of the linear stability [39,214] of solution
(2.163) has shown that perturbations of the transversal component
of the velocity (i.e.
![]() with
with
![]() )
always decay in time, but following an algebraic decay. The details of
the several studies on the linear stability analysis of hydrodynamics
are discussed in the introduction to Chapter V of this work.
)
always decay in time, but following an algebraic decay. The details of
the several studies on the linear stability analysis of hydrodynamics
are discussed in the introduction to Chapter V of this work.
The authors [39] have also studied self-diffusion (i.e. evolution of the
mean displacement of a tagged particle identical to the others) and
Brownian motion (i.e. evolution of the mean displacement of a tagged
particle more massive than the others of the gas) in the Homogeneous
Cooling State. These situations can be studied by means of the
Boltzmann-Lorentz equation that governs the one particle probability
density function ![]() of labeled particles. For granular gases this equation reads:
of labeled particles. For granular gases this equation reads:
or otherwise (when the labeled particle has a mass very much greater
than the mass of the other particles) to a Fokker-Planck equation
(which has the advantage of being a linear equation in ![]() ).
).
The authors have verified that the self-diffusion coefficient obtained
by a Chapman-Enskog solution of the Boltzmann-Lorentz equation is
consistent with Molecular Dynamics and Direct Simulation Monte Carlo
solutions of the same equation. The study of the Brownian Motion has
also indicated that, for a wide range of dissipation values (![]() )
the classical picture called ``aging to hydrodynamics'',
i.e. microscopic modes decaying faster then the macroscopic ones and
the long time evolution described by the hydrodynamic mode, is still
valid.
)
the classical picture called ``aging to hydrodynamics'',
i.e. microscopic modes decaying faster then the macroscopic ones and
the long time evolution described by the hydrodynamic mode, is still
valid.
The hydrodynamics contained in Eqs. (2.160) and in the closure
relations (2.161) is limited to dilute situations, as can
be also intuited observing that the scalar pressure has been kept in
its dilute form (![]() ) and that the bulk viscosity
) and that the bulk viscosity ![]() (see
paragraph 2.3.9) is neglected. Even if in
principle there are no restrictions in the inelasticity parameter, the
equations of Brey and co-workers can become unreliable at high
inelasticities because of strong density fluctuations: the total
volume fraction, in fact, can become poorly representative of the
local volume fraction, so that the diluteness in the initial condition
may fail.
(see
paragraph 2.3.9) is neglected. Even if in
principle there are no restrictions in the inelasticity parameter, the
equations of Brey and co-workers can become unreliable at high
inelasticities because of strong density fluctuations: the total
volume fraction, in fact, can become poorly representative of the
local volume fraction, so that the diluteness in the initial condition
may fail.
Some authors have given alternative closure relations, valid also in
more dense regimes, in particular focusing on the equation of state of
the gas that is the closure expression relating the scalar pressure
![]() to the density and temperature fields (see for
example [102,149,202]). One important result
obtained for example is that the inelasticity parameter appears in
these extended equations of state always to multiply a term of order
to the density and temperature fields (see for
example [102,149,202]). One important result
obtained for example is that the inelasticity parameter appears in
these extended equations of state always to multiply a term of order
![]() , i.e. inelasticities corrections to the pressure are
subleading terms and therefore negligible in dilute systems.
, i.e. inelasticities corrections to the pressure are
subleading terms and therefore negligible in dilute systems.
At the same time, another groups of authors [214] have investigated the physics of granular gases at a more basic levels, i.e. at the kinetic level. They have derived the ring kinetic equations as well as the Boltzmann-Enskog equation in a rigorous manner (as Brey et al. did in [41]) and have pursued a program of investigation of these equations. A brief outline of the results on the Boltzmann-Enskog equation has been given in paragraph 2.2.8. They have also addressed the emergence of ordered structures, i.e. short and long range correlations, proposing kinetic ordering equations for those processes. These results will be reviewed in the first section of Chapter V.