Corrections at high densities

Next: Granular hydrodynamics Up: The hydrodynamical limit Previous: Burnett and super-Burnett orders Contents

Corrections at high densities

If the Boltzmann-Enskog equation is used as the basic kinetic equation, the transport coefficients and the scalar pressure change. In principle the transport coefficients (and the scalar pressure) can be expanded in powers of the density [109]:

$\begin{subequations}\begin{align}p&=p_{dil}(1+p_2n+p_3n^2+...) \ \eta&=\eta_{d... ...2n^2+...) \ \eta'&=\eta'_2n^2+\eta'_3n^3+... \ \end{align}\end{subequations}$

where $p_{dil}=nk_BT$ is the scalar pressure in the dilute case $n \ll 1$ , $\eta_{dil} \propto \sqrt{mk_BT}$ is the viscosity in the dilute case, $\kappa_{dil} \propto k_B\sqrt{k_BT/m}$ is the heat conductivity in the dilute case and $\eta'$ is the bulk viscosity which has been neglected till now as it is of order $\sim n^2$ . The bulk viscosity modifies the expression for the stress tensor, introduced in Eq. (2.144) i.e.:

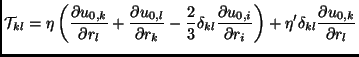$\displaystyle \mathcal{T}_{kl}=\eta\left(\frac{\partial u_{0,k}}{\partial r_l}+... ...}}{\partial r_i}\right)+ \eta'\delta_{kl} \frac{\partial u_{0,k}}{\partial r_l}$

(2.142)

The Enskog correction accounts for the appearance of position correlations at high densities: these correlations render the high order terms important so that they must be included in analytical expressions.

In the corrections are the followings:

$\begin{subequations}\begin{align}p&=\frac{4}{\pi \sigma^2}\phi T[1+2\phi \Xi(\si... ...i(\sigma,n)}{\pi \sigma} \sqrt{\frac{m k_B T}{pi}} \end{align}\end{subequations}$

where $\phi$ is the solid fraction (see paragraph 2.2.6).

Next: Granular hydrodynamics Up: The hydrodynamical limit Previous: Burnett and super-Burnett orders Contents

Andrea Puglisi 2001-11-14