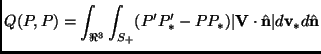 |
(A.1) |
The Direct Simulation Monte Carlo, also known as Bird algorithm, is a simulation scheme useful to solve the Boltzmann equation for gases. The Boltzmann equation is characterized by a linear partial differential operator plus the so-called collision integral (see paragraph 2.2.3):
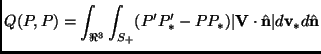 |
(A.1) |
It is a five-dimensional integral that makes difficult numerical
approximations: if we want to approximate this integral by a
quadrature formula, we need the evaluation of the integrand in ![]() points where
points where ![]() is the number of points necessary to well approximate
a one-dimensional integral. For example, if
is the number of points necessary to well approximate
a one-dimensional integral. For example, if ![]() , than we must
evaluate the integrand in
, than we must
evaluate the integrand in
![]() points, at every time step
of our integration algorithm. Particle simulation methods (like the
Bird algorithm) avoid this problem by replacing the density
distribution
points, at every time step
of our integration algorithm. Particle simulation methods (like the
Bird algorithm) avoid this problem by replacing the density
distribution ![]() by a discrete measure of test particles, the
so-called ``simulation gas''. The number of test particles can be
anything between
by a discrete measure of test particles, the
so-called ``simulation gas''. The number of test particles can be
anything between ![]() and several millions, depending on the capacity
of the computer being used. The key idea of particle simulations stems
from the consideration that the physical reality underlying the
problem is a gas with, say,
and several millions, depending on the capacity
of the computer being used. The key idea of particle simulations stems
from the consideration that the physical reality underlying the
problem is a gas with, say, ![]() particles and that the Boltzmann
equation is only a mathematical approximation to this reality: the use
of this equation is a drastic reduction of the number of freedom
degrees (even if it replaces a finite number of degrees with a
six-dimensional infinite number of them, we can consider the Boltzmann
equation the result of a compression of information), and
therefore we can replace it with some other kind of approximation that
reduces the number of freedom degrees. Therefore, in particle
simulations we return to the particle level, but restrict the number
of particles in order to make it tractable, and consequently change
the interaction rules in order to make them reflect the influence of
the collisions on the behavior of the gas.
particles and that the Boltzmann
equation is only a mathematical approximation to this reality: the use
of this equation is a drastic reduction of the number of freedom
degrees (even if it replaces a finite number of degrees with a
six-dimensional infinite number of them, we can consider the Boltzmann
equation the result of a compression of information), and
therefore we can replace it with some other kind of approximation that
reduces the number of freedom degrees. Therefore, in particle
simulations we return to the particle level, but restrict the number
of particles in order to make it tractable, and consequently change
the interaction rules in order to make them reflect the influence of
the collisions on the behavior of the gas.
The Bird scheme [29,30] has been successfully employed for the simulation of rarefied gases for decades (for example in the calculations for the reentry of spacecrafts). Recently non constructive [218] and constructive [185] proofs of its convergence to the solution of the Boltzmann equation have been given.
The scheme consists of the following ingredients:
This means that the particles evolve independently for a time ![]() and then the p.d.f.
and then the p.d.f. ![]() is modified in order to take into account
the collision, by evaluating the integral
is modified in order to take into account
the collision, by evaluating the integral ![]() (this is the difficult part).
(this is the difficult part).
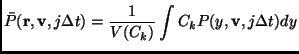 |
(A.3) |
and therefore also ![]() is homogeneous on the cells
is homogeneous on the cells ![]() of
volume
of
volume ![]() . The free flow step in Eq. (79b) will destroy
the local homogeneity. We assume that all the cells
. The free flow step in Eq. (79b) will destroy
the local homogeneity. We assume that all the cells ![]() have the same
diameter and call it
have the same
diameter and call it ![]() (
(![]() stays for Bird but also for Boltzmann,
so that
stays for Bird but also for Boltzmann,
so that ![]() is called Bird radius or Boltzmann radius
indifferently). The local homogenization is important for both
practical and conceptual reasons: it makes more easy (and rapid) to
simulate the collisions among particles and, at the same time,
fulfills the Boltzmann idea that the spatial variation of the particle
density over a cell with volume
is called Bird radius or Boltzmann radius
indifferently). The local homogenization is important for both
practical and conceptual reasons: it makes more easy (and rapid) to
simulate the collisions among particles and, at the same time,
fulfills the Boltzmann idea that the spatial variation of the particle
density over a cell with volume ![]() could be neglected: it is
the velocity dependence of the particles in such a cell that would
make a difference.
could be neglected: it is
the velocity dependence of the particles in such a cell that would
make a difference.
Here follows the algorithm, step by step:
 |
with ![]() a normalization constant.
a normalization constant.
We have used a slight different scheme where the particles in the
cells have a fixed a-priori probability ![]() of colliding
during a time step
of colliding
during a time step ![]() : every particle is checked for
collision, throwing a random number in the range
: every particle is checked for
collision, throwing a random number in the range ![]() ; if the
number is lesser than
; if the
number is lesser than ![]() then the particle is admitted for
collision (it is particle
then the particle is admitted for
collision (it is particle ![]() ) and a collision mate
) and a collision mate ![]() is chosen
in the cell with probability
is chosen
in the cell with probability
![]() . In a homogeneous situation
with
. In a homogeneous situation
with ![]() of the order of the mean free path, this guarantees that
the mean free time is about
of the order of the mean free path, this guarantees that
the mean free time is about
![]() .
.
To study more dense situations, alternative schemes have been proposed that take into account spatial density correlations in a way consistent with the Enskog correction to the Boltzmann equation [90,165,166].