Next: Papers Up: thesis Previous: Appendix A - The Contents

Appendix B - Coefficients of granular hydrodynamics of 2D Inclined Plane Model

In section 4.4 the hydrodynamics of the first model is studied. The equations with the transport coefficients calculated by Brey et al. [43] are used. The coefficients needed in our case are the two thermal conductivities $\kappa$ and $\mu$ appearing in the expression of the heat flux

$\displaystyle {\bf q}=-\kappa {\bf\nabla}T-\mu {\bf\nabla}n$

(B.1)

and the coefficient $\zeta$ of the dissipative term

$\displaystyle -\zeta k_BT.$

(B.2)

In reference [39] the coefficients are given for the case ( is the dimension of the space). We have taken the coefficients for from an unpublished (to our knowledge) work of Brey et al. They have been subsequently published it in [43] and we summarize their results here:

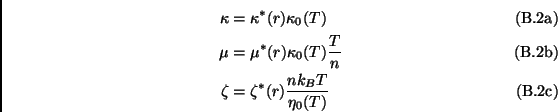$\begin{subequations}\begin{align}\kappa&=\kappa^*(r)\kappa_0(T) \ \mu&=\mu^*(r... ...{T}{n}\ \zeta&=\zeta^*(r)\frac{nk_BT}{\eta_0(T)} \end{align}\end{subequations}$

where $\kappa_0(T)$ and $\eta_0(T)$ are the heat conductivity and viscosity coefficients respectively for elastic hard disks. In the limit $r \to 1$ the numerical coefficient $\kappa^*$ tends to , while $\mu^*$ and $\zeta^*$ vanish. We have:

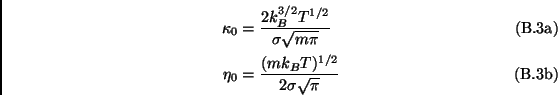$\begin{subequations}\begin{align}\kappa_0&=\frac{2k_B^{3/2}T^{1/2}}{\sigma \sqrt... ... \eta_0&=\frac{(mk_BT)^{1/2}}{2\sigma\sqrt{\pi}} \end{align}\end{subequations}$

The expression for the numerical coefficients are the following:

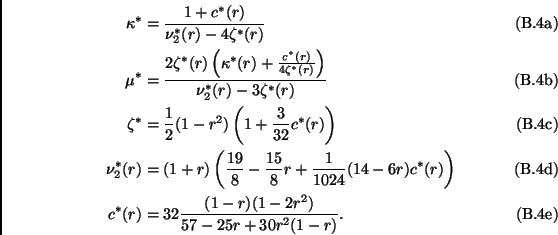$\begin{subequations}\begin{align}\kappa^*&=\frac{1+c^*(r)}{\nu_2^*(r)-4\zeta^*(r... ...c^*(r)&=32\frac{(1-r)(1-2r^2)}{57-25r+30r^2(1-r)}. \end{align}\end{subequations}$

In section 4.4 we have used the following re-definitions of the above coefficients:

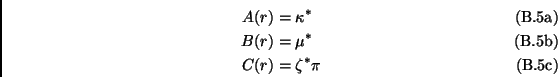$\begin{subequations}\begin{align}A(r)&=\kappa^*\ B(r)&=\mu^*\ C(r)&=\zeta^* \pi \end{align}\end{subequations}$

Next: Papers Up: thesis Previous: Appendix A - The Contents

Andrea Puglisi 2001-11-14