The Burgers hypothesis
In a recent paper, Ben-Naim et al. [22] have studied the
cooling granular gas in ![]() , discovering that, after the homogeneous
(Haff) phase, it asymptotically becomes independent of the value of
inelasticity
, discovering that, after the homogeneous
(Haff) phase, it asymptotically becomes independent of the value of
inelasticity ![]() and maps onto the sticky gas model (that in
and maps onto the sticky gas model (that in
![]() is equivalent to the cooling granular gas with
is equivalent to the cooling granular gas with ![]() ,
i.e.
,
i.e.
![]() ). For such a sticky gas the temperature
decays as
). For such a sticky gas the temperature
decays as ![]() . Moreover, this gas shows instability in the
density and velocity profiles: density clusters and velocity shocks
form. The cooling gas in
. Moreover, this gas shows instability in the
density and velocity profiles: density clusters and velocity shocks
form. The cooling gas in ![]() become asymptotically equivalent to a
sticky gas [57], for any value of
become asymptotically equivalent to a
sticky gas [57], for any value of ![]() , because of
the formation of clusters: when the cluster size (number of particles
belonging to it) has reached the critical value
, because of
the formation of clusters: when the cluster size (number of particles
belonging to it) has reached the critical value
![]() , a particle colliding with the cluster is absorbed,
i.e. never emerges from it. The
, a particle colliding with the cluster is absorbed,
i.e. never emerges from it. The ![]() regime lasts until all the
particles have fallen in one big cluster and the kinetic energy
becomes constant. The authors have verified their idea with MD
simulations, using a trick to avoid inelastic collapse: every time two
particles collide with an absolute relative velocity lesser than
regime lasts until all the
particles have fallen in one big cluster and the kinetic energy
becomes constant. The authors have verified their idea with MD
simulations, using a trick to avoid inelastic collapse: every time two
particles collide with an absolute relative velocity lesser than
![]() , the collision is assumed to be elastic. They have verified
that the results of MD simulations are independent of the value of
, the collision is assumed to be elastic. They have verified
that the results of MD simulations are independent of the value of
![]() . As the sticky gas is described by the inviscid (the
kinematic viscosity
. As the sticky gas is described by the inviscid (the
kinematic viscosity
![]() ) limit of the Burgers equation [199]:
) limit of the Burgers equation [199]:
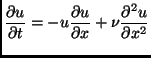 |
(5.29) |
the velocity profile can be predicted to be discontinuous, with shocks
(i.e. asymmetric discontinuities shown in Fig. fig_shocks) in
correspondence with the clusters of the gas. The relation to the
Burgers equation is useful also to establish an estimate of the tails
of the asymptotic velocity distribution
![]() (independent of
(independent of ![]() ), which reads
), which reads
![]() . The MD simulations have revealed very slight deviations
from the Gaussian, and the authors have imputed the discrepancy from
the expected behavior to the smallness of the constant in front of
. The MD simulations have revealed very slight deviations
from the Gaussian, and the authors have imputed the discrepancy from
the expected behavior to the smallness of the constant in front of
![]() . Finally, Ben-Naim et al. have conjectured that the Burgers
equation describes the flow velocity
. Finally, Ben-Naim et al. have conjectured that the Burgers
equation describes the flow velocity
![]() of a
cooling granular gas for arbitrary values of the inelasticity
of a
cooling granular gas for arbitrary values of the inelasticity
![]() in generic
in generic ![]() dimensions, i.e.:
dimensions, i.e.:
where ![]() is the kinematic viscosity and the solutions are looked in
the rotation-free class
is the kinematic viscosity and the solutions are looked in
the rotation-free class
![]() . This conjecture implies that the asymptotic behavior of
the cooling inelastic gas is independent of
. This conjecture implies that the asymptotic behavior of
the cooling inelastic gas is independent of ![]() (as it always
falls in the universality class of the sticky gas) and that the upper
critical dimension for the disappearance of the inelastic collapse is
(as it always
falls in the universality class of the sticky gas) and that the upper
critical dimension for the disappearance of the inelastic collapse is
![]() . The simplest objection to this conjecture comes from the
consideration that in
. The simplest objection to this conjecture comes from the
consideration that in ![]() the
the ![]() case is equivalent to the sticky
gas, while in
case is equivalent to the sticky
gas, while in ![]() the
the ![]() is not equivalent, as normal component
of the relative velocity are in principle different from zero after a
collision.
is not equivalent, as normal component
of the relative velocity are in principle different from zero after a
collision.
The TDGL hypothesis
In another interesting paper, Wakou et al. [219] have
demonstrated that the evolution of the flow field of a granular fluid,
neglecting the convective term
![]() , can be cast in the form of a Time
Dependent Ginzburg-Landau equation for a non-conserved order parameter
, can be cast in the form of a Time
Dependent Ginzburg-Landau equation for a non-conserved order parameter
![$\displaystyle =(\gamma_0+D \nabla^2)\mathsf{S}-\frac{2}{d}D\overline{\vert S\vert^2}S=-V \frac{\delta\mathcal{H}[\mathsf{S}]}{\delta \mathsf{S}^\dagger}$](img1517.png) |
(5.31) | |
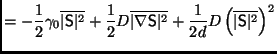 |
(5.32) |
with
![]() independent of time, and the tensorial order
parameter
independent of time, and the tensorial order
parameter
![]() (e.g.
tr
(e.g.
tr![]() )
)
![]() the rescaled velocity field.
the rescaled velocity field.
It is useful to report Equation (5.33) in Fourier space:
![$\displaystyle = \left\{\gamma_0-Dk^2-\frac{2D}{dV^2}\sum_{\mathbf{q}}\vert\math...
...}=-V^2\frac{\delta\mathcal{H}[\mathsf{S}]}{\delta\mathsf{S}^\dagger_\mathbf{k}}$](img1525.png) |
(5.33) | |
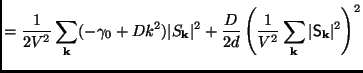 |
(5.34) |
The typical form of the Ginzburg-Landau equation of motion for a
non-conserved order parameter can be recognized:
![]() with
with
![]() . The Landau
free energy functional
. The Landau
free energy functional
![]() has a quartic term
has a quartic term
![]() and a quadratic term
and a quadratic term
![]() . It differs from the standard
Landau free energy in that the quartic term contains summations over
two totally independent wave numbers.
. It differs from the standard
Landau free energy in that the quartic term contains summations over
two totally independent wave numbers.
The energy functional has a continuous set of degenerate minima,
having the shape of a Mexican hat. However the above considerations
have been made neglecting the convective term of the hydrodynamics
equations. When this term is added, only subsets of admissible
solutions are selected out of this infinite set of minima. In two
dimensions only two distinct minima survive: therefore the ![]() cooling granular gas, during the formation of instabilities, greatly
resembles the spinodal decomposition for a non-conserved order
parameter (Model A universality class, in the Hohenberg-Halperin
classification [110]).
cooling granular gas, during the formation of instabilities, greatly
resembles the spinodal decomposition for a non-conserved order
parameter (Model A universality class, in the Hohenberg-Halperin
classification [110]).
The pseudo-Maxwell molecules model
Another approach to the study of cooling granular gas, as we have already discussed, is the study of the kinetic equation, assuming that some form of (Boltzmann or Boltzmann-Enskog) Molecular Chaos hypothesis holds. Some authors (Ben-Naim et al [24], Bobylev et al. [33]) have conjectured the possibility of get an insight on the kinetics of granular gas using a modification of the Boltzmann equation, i.e. using the Maxwell molecules model with inelasticity, usually referred to as the pseudo-Maxwell model. The connection between Maxwell model and granular kinetics has been conjectured by Bobylev et al. on the basis of heuristic considerations. We quote a passage from their article appeared on Journal of Statistical Physics [33]: the Equation (2.98) ``is often considered as the basic kinetic equation for granular media. On the other hand, this equation is a fairly rough mathematical model of a real physical process. Even without mentioning rotational effects and deviations from spherical shape of particles, one can realize that the formula'' (2.98) ``is very rough outside of the Boltzmann-Grad limit. This formula certainly does not account for non-Markovian effects of repeating collisions. Moreover, the model of inelastic scattering based on empirical restitution coefficient is also a very rough approximation. Thus we have the equation'' (2.98) ``which is (a) a very rough approximation from physical point of view and (b) quite complicated equation from mathematical point of view. These obvious considerations lead to the idea of using a simplified version of Eq. `` (2.98). It must be noted that Bobylev et al. refer to the Enskog-Boltzmann equation, i.e. to Eq. (2.98) with the Enskog corrections to the Molecular Chaos hypothesis (and with exact dependence on positions).
The simplification suggested is the following:
to be put in the Boltzmann (or Enskog-Boltzmann) equation (![]() is an
appropriate constant). The assumption (5.37)
leads to a dramatic simplification of the collisional integral
is an
appropriate constant). The assumption (5.37)
leads to a dramatic simplification of the collisional integral
![]() , which (in the absence of Enskog corrections) becomes:
, which (in the absence of Enskog corrections) becomes:
In the Boltzmann equation it appears multiplied by a factor
![]() . As discussed in section
2.2, this is analogous to the collisional
integral of the Maxwell molecules model, as there is no dependence on
the relative velocity in the scattering cross section. This model of
kinetic equation is called pseudo-Maxwell model, as it concerns inelastic hard-core collisions.
. As discussed in section
2.2, this is analogous to the collisional
integral of the Maxwell molecules model, as there is no dependence on
the relative velocity in the scattering cross section. This model of
kinetic equation is called pseudo-Maxwell model, as it concerns inelastic hard-core collisions.
Bobylev and co-workers have studied this model obtaining some theorems of existence and uniqueness of self-similar homogeneous asymptotic solutions and interesting relations among coefficients of Taylor expansion of the characteristic function for the asymptotic solution. They have also discussed the hydrodynamics (Euler) equations and their linear stability, finding again long wave-length instabilities. We discuss some of their result in paragraph 5.3.
It is also noticeable that the pseudo-Maxwell model with the (ideal)
assumption of homogeneous density and perfectly uncorrelated colliding
particles is analogous to another model, introduced some years ago by
S. Ulam [208], in order to clarify the emergence of Maxwellian
statistics in perfectly elastic gases. The model consists of a set of
![]() ``energies'' with the following discrete evolution: at every time
step a pair of energies is chosen at random and their kinetic energy
is randomly re-distributed with the constraint that the sum is
conserved. The asymptotic distribution of energies, independently of
the starting distribution, is Maxwellian. The homogeneous
pseudo-Maxwell model can be considered the inelastic counterpart of
this Ulam model.
``energies'' with the following discrete evolution: at every time
step a pair of energies is chosen at random and their kinetic energy
is randomly re-distributed with the constraint that the sum is
conserved. The asymptotic distribution of energies, independently of
the starting distribution, is Maxwellian. The homogeneous
pseudo-Maxwell model can be considered the inelastic counterpart of
this Ulam model.
Ben-Naim and Krapivsky [24] have studied the same model
considering scalar velocities (as in ![]() ) in an infinitely connected
topology (every particle can collide with every other particle, as in
Ulam model), discovering that the asymptotic solution exhibits
multiscaling, i.e. the moments of the solving distribution increase in
time with different exponents, coming to the wrong conclusion that
there is not a scaling solution
) in an infinitely connected
topology (every particle can collide with every other particle, as in
Ulam model), discovering that the asymptotic solution exhibits
multiscaling, i.e. the moments of the solving distribution increase in
time with different exponents, coming to the wrong conclusion that
there is not a scaling solution
![]() . We have found a correct
scaling asymptotic solution for this model in
. We have found a correct
scaling asymptotic solution for this model in ![]() and verified, with
numerical simulations, that it is reached by a very general class of
initial distribution. This is discussed in the third section of the
chapter.
and verified, with
numerical simulations, that it is reached by a very general class of
initial distribution. This is discussed in the third section of the
chapter.