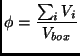Vibration induced compaction and glassy granular systems

Another frontier of the experimental granular physics is the problem of vibration induced compaction: the granular material poured in a container (for example a simple box) quickly reaches the equilibrium, i.e. the balance of all internal and external forces. At that point one can measure the volume fraction, or packing fraction, i.e. the ratio:

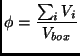$$\phi=\frac{\sum_i V_i}{V_{box}}$$ (1.9)

where the $V_i$ are the volumes of the grains and $V_{box}$ is the volume of the container measured up to the maximum (or average) height reached by the material. The packing fraction measured [174] at the end of the filling, for spheres, has been estimated to be bounded by the limiting values $\phi_{min}=0.55$ and $\phi_{max}=0.64$. After the initial filling, some external force, i.e. a vibration, can change the arrangement of grains and therefore its volume fraction, usually increasing it. S. F. Edwards and A. Mehta [160,64] have proposed a new formalism that resembles thermodynamics and that describes the evolution of a granular system subject to slow vibration: in this formalism the energy is the occupied volume $V$ and the Hamiltonian is a functional $W$ that gives the occupied volume if applied to a certain configuration (spatial positions) of the grains. The granular system is assumed to evolve through states of equilibrium (in this new thermodynamics). The entropy $S$ is defined as the logarithm of the number of possible configurations with the same occupied volume $V$, while the temperature is substituted by the ``compactivity'' $X$ which is defined as

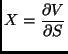$$X=\frac{\partial V}{\partial S}$$ (1.10)

With this formalism, Barker and Mehta [17] have shown that the relaxation of the volume fraction in response to a continuous sequence of vibrations is fast exponential with two relaxation times associated with collective and individual modes. Another mechanism has been proposed to describe the vibration-induced compaction: in this theory the motion of the voids filling the space between the particles is effectively diffusive and as a result a power-law relaxation is predicted [55,111].

The careful experiment of Knight et al. [126] demonstrated that the vibration-induced compaction (in a tube subject to tapping followed by long pauses) is governed by a logarithmically slow relaxation (see Fig. fig_slow_compaction):

$$\phi(t)=\phi_{f}-\frac{\Delta \phi_{\infty}}{1+B \ln(1+t/\tau)}$$ (1.11)

where the parameters $\phi_f$, $\Delta \phi_{\infty}$, $B$ and $\tau$ depend only on the acceleration parameter $\Gamma$ that is the ratio between the peak acceleration of a tap and the gravity acceleration $g$. The discover of this inverse logarithmic behavior (very slow with respect to previous predictions) has motivated the introduction of new models and has also attracted the interest of specialists of other fields: in particular the slow relaxation is a typical phenomenon observed in glassy states of matter, e.g. the aging in amorphous solids like glasses.

Figure 1.3: Slow Compaction: the packing fraction vs. time (in units of taps)

Figure 1.4: An example configuration of the Tetris-model

E. Ben-Naim et al. [23] have explained the slow relaxation law (1.11) in terms of a simple stochastic adsorption-desorption process: the desorption process is unrestricted and happens with a well defined rate, while the adsorption process is restricted by the occupied volume, i.e. new particles cannot be adsorbed on top of previously adsorbed particles. This model has been also called car parking model, as it reproduces the increasing difficulty of parking a car in a parking lot as the number of parked cars get larger and larger. The inverse logarithmic law has been recovered solving this model.

Another way, perhaps more realistic, of recovering the inverse logarithmic relaxation, is described by Caglioti et al. [50,49] by means of a ``Tetris-like'' model (displayed in Fig. fig_tetris). In this model the grains are represented by objects disposed on a regular lattice: the different shapes of the objects induce geometrical frustration, i.e. some kinds of grains cannot stay near some other kinds of grains and therefore the equilibrium configuration of a filled box is disordered and present a random packing fraction: a computer simulation of the vibration dynamics (short periods of tapping followed by long periods of undriven rearrangement until the new equilibrium is reached) shows that this model reproduces the inverse logarithmic relaxation. The study of this model has shed light on many features of the dynamics of dense granular media, such as vibration-induced segregation, bubbling and avalanches. Moreover, the possibility of mapping the dynamics of the Tetris model onto that of a Ising-like spin system with vacancies has introduced a new bridge between the physics of granular media and that of disordered systems (like spin glasses and structural glasses). In particular the interest of researchers has focused on the following remarkable fact: spin glass models [164,28] (such as the Sherrington- Kirkpatrick [200] model or the Edwards-Anderson model [78]) always contain a quenched (frozen) disorder, usually given by the set of $J$'s that weight the interactions among spins. A dense granular media evolve without any frozen disorder, nevertheless its dynamics presents many ``glassy'' features (such as history dependence of the dynamics, hysteresis, frustration, metastable equilibria and so on) [170,18]. This consideration is at the base of all the recent studies on spin lattice models without quenched disorder. It must be said that many of these models have little in common with the real granular materials and are often more useful tools in the study of the behavior of spin or structural glasses.