Janssen effect and the distribution of internal stresses

In 1895 H. A. Janssen [118] discovered that in a vertical cylinder the pressure measured at the bottom does not depend upon the height of the filling, i.e. it does not follow the Stevin law which is valid for Newtonian fluids at rest [137]:

$$p_v(h)=\rho g h$$ (1.1)

where $p_v$ is the vertical pressure, $\rho$ the density of the fluid, $g$ the gravity acceleration and $h$ the height of the column of fluid above the level of measurement. The pressure in the granular material follows instead a different law, which accounts for saturation:

$$p_v(h)=\Lambda \rho g - (\Lambda \rho g-p_v(0))\exp(-h/\Lambda)$$ (1.2)

where $\Lambda$ is of the order of the radius $R$ of the cylinder. This guarantees the flow rate in a hourglass to be constant. Moreover, this law is very important in the framework of silos building, as the difference between ordinary hydrostatic and granular hydrostatic is mainly due to the presence of anomalous side pressure, i.e. force exerted against the walls of the cylinder. It happens that the use of a fluid-like estimate of the horizontal and vertical pressure leads to an underestimating of the side pressure and, consequently, to unexpected (and dramatic) explosions of silos [128].

The first interpretation of the law has been given by Janssen in his paper, in terms of a simplified model with the following assumptions:

1. The vertical pressure $p_v$ is constant in the horizontal plane.

2. The horizontal pressure $p_h$ is proportional to the vertical pressure $p_v$ where $K=p_h/p_v$ is constant in space.

3. The wall friction $f=\mu p_h$ (where $\mu$ is the static friction coefficient) sustains the vertical load at contact with the wall.

4. The density $\rho$ of the material is constant over all depths.

In particular the first assumption is not true (the pressure depends also upon the distance from the central axis of the cylinder) but is not essential in this model (as it is formulated as a one-dimensional problem), while the second assumption should be obtained by means of constitutive relations, i.e. it requires a microscopic justification.

Imposing the mechanical equilibrium of a disk of granular material of height $dh$ and radius $R$ (the radius of the container) the following equation is obtained:

$$\pi R^2 \frac{d p_v}{d h}dh+2\pi R\mu K p_v dh=\pi R^2 \rho g dh$$ (1.3)

which becomes:

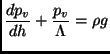$$\frac{d p_v}{dh}+\frac{p_v}{\Lambda}=\rho g$$ (1.4)

where $\Lambda=\frac{R}{2\mu K}$. This equation is exactly solved by the function (1.2).

Figure 1.1: Force chains generated after a localized (on top) perturbation

The particular behavior of the vertical pressure in granular materials is mainly due to the anomalies in the stress propagation. The configuration of the grains in the container is random and the weight can be sustained in many different ways: every grain discharges its load to other grains underlying it or at its sides, creating big arches and therefore propagating the stress in unexpected directions. Moreover, arching is not only a source of randomness, but also of strong fluctuations, i.e. disorder: in a granular assembly some force chains can be very long and span the size of the entire system, posing doubts on the validity of (local) mean field modeling.

Further interesting phenomena have been experimentally observed in the statics of granular materials:

• the fluctuations of the pressure at the bottom of a silo are large, they can change of more than $20\%$ in repeated pouring of grains in the same container [48], and in a single pouring the distribution of stresses, measured deep inside or at the bottom of the silo, show an exponential tail [141,168,46].

• the vertical pressure below conical sandpiles does not follow the height of the material, but rather has a minimum underneath the apex of the pile [217]

Different models have been proposed and debated in the last years, in order to understand the problem of the distribution of forces in a silo or in a granular heap.

The q-model has been introduced in 1995 (remarkably a century after the work of Janssen) by Liu et al. [141,66] in order to reproduce the stress probability distribution observed in experiments. The model consists of a regular lattice of sites each with a particle of mass unity. Each site $i$ in layer $D$ is connected to exactly $N$ sites $j$ in layer $D+1$. Only the vertical components of the forces $w=\sigma_{zz}$ are considered explicitly: a random fraction $q_{ij}(D)$ of the total weight supported by particle $i$ in layer $D$ is transmitted to particle $j$ in layer $D+1$. Thus the weight supported by the particle in layer D at the $i$-th site, $w(D,i)$, satisfies a stochastic equation:

$$w(D+1,j)=1+\sum_i q_{ij}(D)w(D,i)$$ (1.5)

The random variables $q_{ij}(D)$ are taken independent except for the constraint

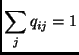$$\sum_jq_{ij}=1$$ (1.6)

which enforces the condition of force balance on each particle. Given a distribution of $q$'s, it can be obtained the probability distribution $Q_D(w)$ of finding a site that bears a weight $w$ on layer $D$. By means of mean field calculations, exact calculations and numerical solutions, the authors conclude that (apart of some limiting cases) a generic continuous distributions of $q$'s lead to a distribution of weights that, normalized to the mean, is independent of depth at large $D$ and which decays exponentially at large weights. They find also a good agreement with molecular dynamics simulations of the packing of hard spheres. The q-model has many limits:

• it is a scalar model, i.e. it takes into account only one component of the internal stress (this was solved by P. G. de Gennes [72] who introduced a vectorial version of the q-model, obtaining a more realistic propagation of forces)

• it does not reproduce the minimum (the ``dip'') of the pressure measured under central axis at the bottom of a sand heap

• it does not reproduce the Janssen law [154]; this problem appears as a consequence of the diffusive nature of the q-model solution: the saturation depth $D_s$ where the stress distribution becomes independent of depth scales with the silo width $R$ as $D_s \sim R^2$, at odds with the Janssen observation that predicts $D_s \equiv \Lambda \sim R$.

A more refined version of the Janssen model has been introduced by Bouchaud et al. [36]: the authors have considered a local version of the Janssen assumption on the proportionality between horizontal and vertical stresses:

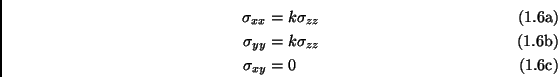which lead to the linear equation:

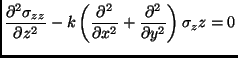$$\frac{\partial^2 \sigma_{zz}}{\partial z^2}-k\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\right)\sigma_zz=0$$ (1.8)

This equation for the vertical stress is hyperbolic and therefore differs from the equivalent equation for an elastic medium, which is elliptic [136], and from the q-model equation that is parabolic (as a diffusion equation): it is equivalent to the equation for the wave propagation with $z$ as the ``time'' variable and $k$ as the inverse of the propagation velocity. This model well reproduces the dip in the measure of the pressure under the bottom of the conical heap [217]. A cellular automaton was introduced by Hemmingsson [106] which was capable of reproduce the dip under the heap as well as the correct Janssen law (with the linear scaling).

Figure 1.2: Propagation of sound

In the framework of the study of force networks in the bulk of a static arrangement of grains a key role was played by the experiments on the propagation of sound. The inhomogeneities present inside a granular medium can drastically change the propagation of mechanical perturbations. Liu and Nagel [139,140,138] have addressed this issue in several experiments. They have discovered [139] that the in the bulk of a granular medium perturbed by a harmonic force ($4$ Hz) the fluctuations could be very large, measuring power-law spectra of the kind $1/f^{\alpha}$ with $\alpha=2.2 \pm 0.05$. Then they have seen [140] that the sound group velocity can reach $5$ times the phase velocity and that a change in the amplitude of vibration can result in a hysteretic behavior (due to a rearrangement of force chains). They have also measured [138] a $25\%$ variation of the sound transmission as a consequence of a very small (compared to the size of the grains) thermal expansion of a little carbon resistor substituted to a grain of the granular medium. This sensitivity to perturbation is another signature of the strong disorder (arching and chain forces) in the bulk of the medium.