The ``Baldassarri solution'' in $d=1$

In a stimulating paper, Ben-Naim and Krapivsky [24] considered such scalar model, and obtained the evolution of the moments of the velocity distributions. They found a multiscaling behavior, i.e.. at large times

$$\left<v^n\right>\sim \exp(-\tau a_n)$$ (5.44)

and the decay rates $a_n \neq na_2/2$ (they depend non-linearly on $n$). They argued that such a multiscaling behavior prevents the existence of a rescaled asymptotic distribution, i.e. that it was not possible to find a function $f$ such that

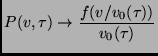$$P(v,\tau)\to \frac{f(v/v_0(\tau))}{v_0(\tau)}$$ (5.45)

for large $\tau$, where

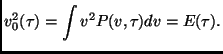$$v_0^2(\tau)=\int v^2 P(v,\tau)dv=E(\tau).$$ (5.46)

On the contrary, we believe that such a ``multiscaling'' behavior only indicates the fact that the moments of the rescaled distribution

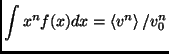$$\int x^n f(x) dx=\left< v^n\right>/v_0^n$$ (5.47)

diverge asymptotically for $n\ge 3$, and does not rule out the possibility of the existence of an asymptotic distribution with power law tails.

The Fourier transform of Eq. (5.46) reads

$$\partial_\tau \hat{P}(k,\tau)+\hat{P}(k,\tau)=\hat{P}[ k/(1-\beta),\tau]\hat{P}[k/\beta,\tau]$$ (5.48)

It possesses several self-similar solutions of the kind

$$\hat{P}(k,\tau)=\hat f(k v_0(\tau))$$ (5.49)

which correspond to the asymptotic rescaled distribution

$$P(v,\tau)=f(v/v_0(\tau))/v_0(\tau)$$ (5.50)

Many self-similar solutions do not correspond to physically acceptable velocity distributions. The divergence of the higher moments implies a non analytic structure of $\hat f$ in $k=0$, since

$$\left<v^n\right>/v_0^n=(-i)^n \frac{d^n}{dk^n} \hat{f}(k)\vert _{k=0}$$ (5.51)

and represents a guide in the selection of the physical solution.

As shown in Fig. fig_ulamvdist, our data collapse on the function

$$f(v/v_0(\tau))=\frac{2 }{\pi \left[1+(v/v_0(\tau))^2\right]^2}.$$ (5.52)

corresponding to the self-similar solution [14]

$$\hat{f}(k)=(1+\vert k\vert)\exp(-\vert k\vert)$$ (5.53)

Notice that (5.55) is a solution of Eq.(5.46) for every $r < 1$, i.e. this asymptotic velocity distribution does not depend on the value of $r < 1$, as shown in Fig. fig_ulamvdist (left frame).

To conclude, we have checked numerically that the asymptotic scaling distribution in Eq. (5.55) is reached using general starting distributions. We have found that it is reached starting from a Gaussian distribution, from a uniform distribution and from an exponential distribution.

Figure: Asymptotic velocity distributions $P(v,\tau )$ versus $v/v_0(\tau )$ for different values of $r$ from the simulation of the inelastic pseudo-Maxwell (Ulam's) model in 1D (left) and 2D (right). In 1D the asymptotic distribution is independent of $r$ and collapse to the Eq.(5.55), that is ``Baldassarri solution''. The chosen initial distribution is drawn (same result with uniform and Gaussian initial distribution). In 2D the distributions still present power-law tails, but the power depends upon $r$, as shown in the inset: for $r=0$ data are compatible with $\alpha =5$, while for larger $r$, $\alpha$ increases and for $r \to 1$ tends to a Maxwell distribution. Data refers to more than $N=10^6$ particles.