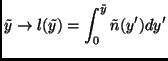 |
(4.24) |
A change of coordinate can be applied to Eqs. (4.22),(4.23) in order to obtain a simpler form:
It follows that when ![]() spans the range
spans the range ![]() , the coordinate
, the coordinate ![]() spans the range
spans the range
![]() . With this change of coordinate it
happens that
. With this change of coordinate it
happens that
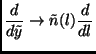 |
(4.25) |
and the first equation (4.22) reads:
from which is immediate to see that
is a constant, i.e.
![]() . This is equivalent to observe
that
. This is equivalent to observe
that
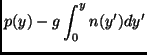 |
(4.28) |
is constant which is nothing more than the Bernoulli theorem for a fluid in the gravitational field with the density depending upon the height.
The relation (4.28) is verified by the model simulated in this work in the Fig. fig:h for almost all the height of the container, apart of the boundary layer near the bottom driving wall.
![\includegraphics[clip=true,width=7cm,keepaspectratio]{pre64_h.ps}](img1335.png) |
Using the coordinate ![]() introduced in (4.25) and the elimination
of
introduced in (4.25) and the elimination
of
![]() using the recognized constant, that is
using the recognized constant, that is
the second equation (4.23), after some simplifications, and after
a second change of coordinate
![]() , becomes:
, becomes:
where
![]() ,
,
![]() are numerically checked to be
positive (
are numerically checked to be
positive (![]() is positive for values of
is positive for values of ![]() not too low, about
not too low, about
![]() ) and are divergent in the limit
) and are divergent in the limit
![]() .
.
The correspondence with the solution of Brey et al. [43] is given by:
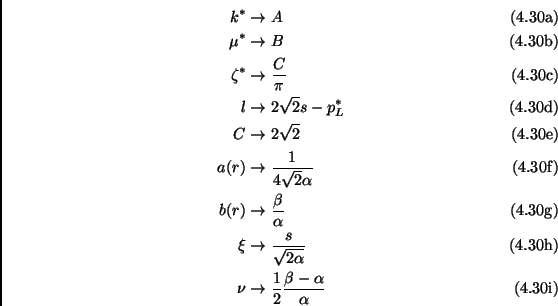 |
The equation (4.31) become a linear equation in
![]() as soon
as the change of variable
as soon
as the change of variable
![]() is performed:
is performed:
giving the solution:
where ![]() and
and ![]() are the modified Bessel functions of the
first kind and the second kind respectively,
are the modified Bessel functions of the
first kind and the second kind respectively,
![]() is real and positive for all the values
of
is real and positive for all the values
of ![]() greater than the zero of the function
greater than the zero of the function ![]() (about
(about
![]() ), with
), with ![]() , while
, while
![]() and
and
![]() are constants that must be determined with assigning the boundary
conditions.
are constants that must be determined with assigning the boundary
conditions.
Then we can derive the expressions for
![]() and
and
![]() :
:
To calculate the expressions of ![]() and
and ![]() as a function of the
original coordinate
as a function of the
original coordinate ![]() one needs to solve the equation
one needs to solve the equation
putting in it the solution (4.36). However one can obtain a
comparison with the numerical simulations using the new coordinate
![]() . For a discussion of the boundary conditions needed to eliminate
the constants
. For a discussion of the boundary conditions needed to eliminate
the constants ![]() ,
,
![]() and
and
![]() we refer the reader
to the paper of Brey et al.[43]. In this paper the authors
show that the solution fit very well a large region in the bulk but
cannot work on the boundary regions near the vibrating bottom and near
the open surface. The authors show also that the minimum of the
temperature is compatible with the proposed equations.
we refer the reader
to the paper of Brey et al.[43]. In this paper the authors
show that the solution fit very well a large region in the bulk but
cannot work on the boundary regions near the vibrating bottom and near
the open surface. The authors show also that the minimum of the
temperature is compatible with the proposed equations.
![\includegraphics[clip=true,width=8cm,keepaspectratio]{pre64_h2.ps}](img1363.png) |