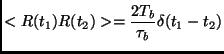Interpretation of the random driving

We have introduced a Langevin equation as the most natural way to model the sum of external driving and external dissipation. In many experimental situations (see section 1.2) this fact has been recognized. One questionable issue is the decision of assume the validity of the fluctuation-dissipation relation (second kind in the Kubo terminology) between dissipation and random accelerations, disregarding the effect of collisions among the grains, i.e.:

$$<R(t_1)R(t_2)>=\frac{2T_b}{\tau_b} \delta(t_1-t_2)$$ (3.7)

that is assumed from each component of Eq. (3.3a) if read as a Langevin equation of the form:

$$\frac{d v(t)}{d t} = -\frac{v_i(t)}{\tau_b} + R(t)$$ (3.8)

The validity of relation (3.7) cannot be guaranteed in a real system of particles kicked by random forces and in the presence of dissipative collisions, as the system is not in thermal equilibrium with the kicking bath. We are studying the possibility of a Langevin description of the whole system (external driving plus inelastic collisions) [16].

It is important to stress that this is a model and its main aim is not to reproduce quantitative details of a real system, but only to make qualitative predictions that can be verified in experiments or can be compared with other models.

To our knowledge, experimental measurements of velocity distributions have been performed only recently (and noticeably only for steady state granular systems under some sort of energy pumping), they have been discussed in section 1.2. We recall some of the real setups used, where non-Gaussian distribution have been observed:

• Vibration of the bottom of a 3D granular system (Losert et al. [144])

• Vertical vibration of an horizontal plate with a granular monolayer on the top of it (Olafsen and Urbach [172,173])

• Vibration of the bottom side of an inclined plane with a very dilute granular monolayer rolling on it, under the presence of gravity (Kudrolli and Henry [132])

• Vibration of the bottom of a granular system confined in a vertical plane (Rouyer and Menon [189])

In paragraph 3.2.6 we discuss the possibility of checking the relevance of the viscous term: it is tied to the velocity correlations. A randomly driven granular gas with a relevant viscosity should not display velocity structures, while they can appear if this term is negligible.