![\includegraphics[clip=true,width=7cm, height=12cm,keepaspectratio]{prl2-fig1-ene.eps}](img1612.png) |
![\includegraphics[clip=true,width=7cm, height=12cm,keepaspectratio]{prl2-fig1-ene.eps}](img1612.png) |
One sees from Fig. fig_endecay that during the initial stage, the total energy per particle
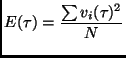 |
(5.58) |
is dissipated at an exponential rate
| (5.59) |
with
![]() , as indicated in formulas
5.6 and 5.5b. The Haff law can be
deduced from Eq.(5.57) imposing that each 'spin' fluctuates
independently of the others. For times larger than
, as indicated in formulas
5.6 and 5.5b. The Haff law can be
deduced from Eq.(5.57) imposing that each 'spin' fluctuates
independently of the others. For times larger than
![]() , of
the order of
, of
the order of
![]() , the system displays a crossover to a
different regime, where the cooperative effects become dominant and
the average energy per particle decay as
, the system displays a crossover to a
different regime, where the cooperative effects become dominant and
the average energy per particle decay as
![]() . Such a behavior agrees with the mode-coupling theory [45]
discussed above (see paragraph 5.1.4) and with the
behavior suggested by inelastic hard spheres simulations (IHSS)
reported in various papers [175,45]. As already
discussed, and as shown below, the crossover from one regime to the
other is due to the formation of a macroscopic velocity field, i.e. to
the shear instability. This is analogous to the formation of domains
in a standard quench processes of magnetic systems. After the
formation stage these regions start to compete to homogenize: this
causes a conversion of kinetic energy into heat by viscous heating. In
the hydrodynamics description of Equation (5.8c),
this is due to the third term, that is the term where the coupling
between the stress tensor
. Such a behavior agrees with the mode-coupling theory [45]
discussed above (see paragraph 5.1.4) and with the
behavior suggested by inelastic hard spheres simulations (IHSS)
reported in various papers [175,45]. As already
discussed, and as shown below, the crossover from one regime to the
other is due to the formation of a macroscopic velocity field, i.e. to
the shear instability. This is analogous to the formation of domains
in a standard quench processes of magnetic systems. After the
formation stage these regions start to compete to homogenize: this
causes a conversion of kinetic energy into heat by viscous heating. In
the hydrodynamics description of Equation (5.8c),
this is due to the third term, that is the term where the coupling
between the stress tensor
![]() and the velocity
gradients
and the velocity
gradients
![]() appear. The viscous heating acts against
the collisional cooling and leads to a slower decay of the
energy.
appear. The viscous heating acts against
the collisional cooling and leads to a slower decay of the
energy.
An interesting observation from Fig. fig_endecay is that the smaller the inelasticity, the higher is the cumulated dissipated energy measured in the second (correlated) regime. This, a phenomenon observed in inelastic hard spheres simulations [158] and is due to the fact that the Haff regime (which is more rapid in dissipating energy) lasts more for less dissipative systems.