Structure factors

Figure: Structure factors $S(k,t)$ against $kt^{2/3}$ for the 1D MD and against $k\tau ^{1/2}$ for the 1D lattice gas model, in the inhomogeneous phase. Times are chosen in the correlated regime, and in such a way that the two systems have the same energies (MD: $t=15,...,316$, lattice model: $\tau =11,...,601$). Data refers to system with more than $N=10^5$ particles, $r=0.5$ (both models).

The Gaussianity of the asymptotic field distribution, and the $\tau ^{-1/2}$ asymptotic decay suggest that, in the lattice model, the scalar velocity field $v(i,\tau )$ is governed by a discretized version of the diffusion equation of the form:

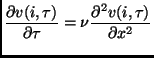$$\frac{\partial v(i,\tau)}{\partial \tau}=\nu \frac{\partial^2 v(i,\tau)}{\partial x^2}$$ (5.40)

This conjecture is analogous to the one made in the previous section for the $d=2$ version of the same model.

We checked this possibility studying the structure factor $S(k,\tau)=\hat{v}(k,\tau)\hat{v}(-k,\tau)$ where $\hat{v}(k,\tau)$ is the Fourier transform of the field $v(i,\tau )$. In fact, at late times, $S(k,\tau)=f_1(k\tau^{1/2})$ scales similarly to a diffusive process as shown by the data collapse in Fig. fig_sf1d (right frame). However the form of the scaling function differs from the Gaussian shape predicted by the diffusion equation.

In the same figure (left) we report the index structure factor of the MD simulation of the Inelastic Hard Rod model, i.e. the Fourier transform of the correlation function in the index space

$$C(r,t)=\langle v(i,t)v(i+r,t) \rangle$$ (5.41)

where $v(i,t)$ is the velocity of the $i$-th particle. In this case a good data collapse, $S(k,t)=f_2(kt^{2/3})$, has been obtained.

The comparison between the two data collapses, i.e. between the two scaling forms obtained, suggests that for both models the correlation length grows as $L(t) \sim E(t)$ or $L(\tau) \sim E(\tau)$, confirming the idea that the physical clock of both system is the energy.

The algebraic tails of the structure factors observed in both models carry important information about the nature of the growing velocity correlations. In particular the power law behavior $S(k) \sim k^{-2}$ is due to the presence of short wavelength defects, viz. shocks, as predicted by Porod's law (for example see [38]).