The decay of energy and the problem of the universal clock

Figure: Time behavior of kinetic energy for the Inelastic Hard Rods (left) and for the Inelastic Lattice Gas (right). The homogeneous Haff stage is evident only for quasi-elastic system, whereas the more inelastic ones enter almost immediately in the correlated regime. Note the different time units used ($t$ or $\tau$). The Haff law $E \sim t^{-2} \sim \exp(-\tau)$ is verified for both systems. The correlated regime presents a behavior $t^{-2/3}$ independent of $r$ for the Hard Rods, while appears diffusive (in collision units) $\tau ^{-1/2}$ and $r$-dependent for the Lattice Gas.

In Fig. fig_endecay1d we report the time behavior of the total energy of the system

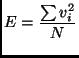$$E=\frac{\sum v_i^2}{N}$$ (5.39)

We use the symbol $t$ to indicate the physical time, while the symbol $\tau$ to indicate the time measured in number of collisions per particle. In the MD simulations the time can be measured in both units, while in the evolution of Inelastic Lattice Gas model the only measure of time is $\tau$.

We observe that initially the energy $E(\tau)$ decreases exponentially in both the models: this corresponds to the law $E(t) \sim t^{-2}$ in the MD simulation, i.e. to the Haff regime, also called Homogeneous Cooling. In the following, we discuss how homogeneous is this first regime, studying its structure factor.

After the formation of long range velocity correlations, the decay slows down, and a power law decay appears for both the models. In the Hard Rods system the decay is of the form $E(t) \sim t^{-2/3}$ , while in the Inelastic Lattice Gas the decay follows $E(\tau) \sim \tau^{-1/2}$, analogous to the decay of energy of a simple diffusion model.

Moreover, the asymptotic decay of the energy for the Hard Rod model, measured in terms of the number of collisions per particle, seems to depend on the regularization discussed above (the elastic cut-off $\delta$), so that a reliable comparison between the observed behaviors is impossible.

It is interesting to note that the $E(t) \sim t^{-2/3}$ law is independent of $r$ (as it is the law $E(\tau) \sim \tau^{-1/2}$ for the Inelastic Lattice Gas), while $E(\tau)$ changes with $r$. It should be explored the possibility if a sort of principle of minimum dissipation (with adequate constraints) governs the asymptotic dynamics: the system organizes itself in order to have a minimum dissipation rate independent of $r$, and do this changing its collision rate (which consequently depends upon $r$).

In general $\tau(t)$ (which makes sense only for the Hard Rod model) is a well defined ``universal'' function for the homogeneous regime only: in the inhomogeneous regime $\tau(t)$ diverges due to the inelastic collapse, or depends on the ``regularization'' of the restitution coefficient.

The problem can be circumvented in many situations, if one assumes the energy, instead of $\tau$, as the physical clock of both dynamics. This allows a direct comparison of other physical measures, such as the structure factors or the velocity distributions. The surprising agreement in this comparison is a nice check of the validity of this ``energy clock''.