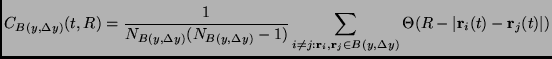Density correlations

In order to characterize the spatial correlations, we have performed an analysis similar to that performed in section 3.2.3, where we observed a fractal clustering phenomena in the Randomly Driven model. In this case we have studied a cumulated particle-particle correlation function defined in this way:

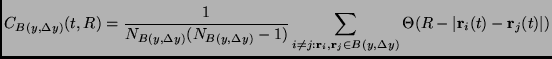$$C_{B(y,\Delta y)} (t,R)=\frac{1}{N_{B(y,\Delta y)}(N_{B(y,\Delta ... ...r}_i,{\bf r}_j \in B(y, \Delta y)}\Theta(R-\vert{\bf r}_i(t)-{\bf r}_j(t)\vert)$$ (4.7)

where $B(y, \Delta y)$ is a horizontal stripe defined by $y \in [y-\Delta y/2,y+\Delta y/2]$ and $x \in [0,L_x]$ . After having checked that the system has reached a stationary regime, we have computed the time-average of the correlation function, that is

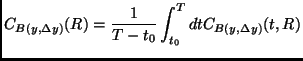$$C_{B(y,\Delta y)} (R)= \frac{1}{T-t_0}\int_{t_0}^T dt C_{B(y,\Delta y)} (t,R)$$ (4.8)

which is independent on time if $T»t_0$. In the Fig. fig:vflip_sc we show the correlation function $C(R)$ vs. $R$ for different stripes $B(y, \Delta y)$. We observe a power law behavior

$$C_{B(y,\Delta y)}(R) \sim R^{d_2(y)}$$ (4.9)

In the case of homogeneous density $d_2$ is expected to be the topological dimension of the box $C_{B(y, \Delta y)}$. This dimension is $d_2=1$ if $R\gg\Delta y$, when the box appears as a ``unidimensional'' stripe and $d_2=2$ if $R\ll\Delta y$, because at close distance it appears as bidimensional.

Figure: Cumulated correlation function C(R), as defined in the text, measured along stripes at different heights for the Inclined Plane Model, with periodically vibrating wall. In the inset is displayed the number density profile, with the position of the chosen stripes. Here $N=500$, $N_w \approx 56$, $r=0.5$, $r_w=0.7$, $f_w=400\pi$, $A_w=0.1$ and $g_e=-1$

Clustering, whose signature is a value of the correlation dimension $d_2$ lower than the topological dimension, appears in some of the analysed stripes: when the density is not too high an exponent smaller than $1$ is measured (the fit is performed in the region $R\gg\Delta y$). Clusters are self similar arrangements of empty spaces alternated with filled spaces: when the particles are too packed (i.e. density is too high) the stripe is somehow filled up and the clustering phenomena disappears.

The evidence of clustering is at odds with the observation of Kudrolli and Henry [132]: they report, in fact, the absence of clustering by measuring the distribution of the number of particles in boxes of fixed dimensions spread all over the inclined plane. This observation is perhaps due to the fact that in the statistical analysis employed in the work of Kudrolli and Henry, the particles are counted in each box disregarding their heights, that is they may belong to regions of different densities which are more or less clusterized: therefore the convolution of different probability distributions with different averages (and different tails) hides the slow decaying tails, expected for the clusterized distributions of the stripes at lower densities. It is also true that, even from the global density distribution measured in their work, a tail decaying slower than a Poissonian cannot be clearly ruled out.