![\includegraphics[clip=true,width=7cm,keepaspectratio]{pre64_flipper.ps}](img1186.png) |
![\includegraphics[clip=true,width=7cm,keepaspectratio]{pre64_flipper.ps}](img1186.png) |
The first model that we study is called ``2D Inclined Plane Model''. It is illustrated in Fig. fig:a_sketch and inspired to recent laboratory experiments [132] and numerical simulations [116]. We have reviewed those experiments in section 1.2.We have shown that in many of them it has been used a closely packed array of grains (for example see [76,181]). Our inspiration has come, instead, from the more dilute setup of Kudrolli and Henry [132], where the velocity distributions and the density correlations have been measured. We have considered that the dilute setup and the measurement performed where better suited to be investigated with our numerical tools, e.g. Direct Simulation Monte Carlo in two dimensions.
Similar models have been previously studied in the one-dimensional
case, that is a vibrated column of grains under the force of
gravity [147,155] and the transition or the
coexistence of different phases (gas, partially fluidized and
condensed) was investigated. In two dimensions
experiments [223], simulations [156] and
theories [134,204] have analyzed a vertical system of
grains with gravity and a vibrating bottom wall (with different kinds
of vibration) searching for a simple scaling relation between global
variables as the global granular temperature ![]() or the center of
mass height
or the center of
mass height ![]() as function of the size of the system
as function of the size of the system ![]() , the
typical velocity of the vibrating wall
, the
typical velocity of the vibrating wall ![]() or the restitution
coefficient
or the restitution
coefficient ![]() . In all these calculations the authors did not pay too
much attention to the hydrodynamic profiles of the system, always
assuming a constant granular temperature (``isothermal atmosphere'') and
a density profile exponentially decaying with the height, as in the
case of a Boltzmann elastic gas under gravity.
. In all these calculations the authors did not pay too
much attention to the hydrodynamic profiles of the system, always
assuming a constant granular temperature (``isothermal atmosphere'') and
a density profile exponentially decaying with the height, as in the
case of a Boltzmann elastic gas under gravity.
The ``apparatus'' consists of a plane of dimension
![]() inclined by an angle
inclined by an angle ![]() with respect to the horizontal. The
particles are constrained to move in such a plane under the action of
an effective gravitational force
with respect to the horizontal. The
particles are constrained to move in such a plane under the action of
an effective gravitational force
![]() pointing
downward. In the horizontal direction there are periodic boundary
conditions: each particle going out from the left or the right border
enters at the same altitude and with the same velocity on the opposite
border. The particles are confined by walls on top and bottom: both
walls are inelastic with a restitution coefficient
pointing
downward. In the horizontal direction there are periodic boundary
conditions: each particle going out from the left or the right border
enters at the same altitude and with the same velocity on the opposite
border. The particles are confined by walls on top and bottom: both
walls are inelastic with a restitution coefficient ![]() . We use, in
general, different restitution coefficients for the particle-particle
interaction and the wall-particle interaction: this is reasonable also
if the wall is covered by stuck grains (as often happens in
experiments), because the microscopic dynamics of a collision with a
stuck grain is completely different from that with a free grain.
. We use, in
general, different restitution coefficients for the particle-particle
interaction and the wall-particle interaction: this is reasonable also
if the wall is covered by stuck grains (as often happens in
experiments), because the microscopic dynamics of a collision with a
stuck grain is completely different from that with a free grain.
The bottom wall vertically vibrates and therefore injects energy and momentum into the system. The vibration can have two different behaviors:
| (4.4) |
where
![]() is the velocity of the
vibrating wall.
is the velocity of the
vibrating wall.
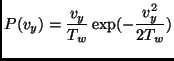 |
(4.5) |
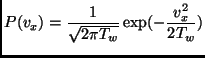 |
(4.6) |