next up previous contents
Next: The boundary conditions of Up: The models Previous: The models   Contents

Equations of motion and collisions

We briefly resume the fundamental definitions of the model. We consider a granular gas in $ d=2$ consisting of $ N$ identical smooth hard disks of diameter $ \sigma $ and mass $ m=1$ subject to binary instantaneous hard-core inelastic collisions which conserve the total momentum

$\displaystyle {\bf v}_1'+{\bf v}_2'={\bf v}_1+{\bf v}_2$ (4.1)

and reduce the normal component of the relative velocity

$\displaystyle ({\bf v}_1'-{\bf v}_2') \cdot {\bf\hat{n}}= -r(({\bf v}_1-{\bf v}_2) \cdot {\bf\hat{n}})$ (4.2)

where $ r$ is the normal restitution coefficient ($ r=1$ in the completely elastic case) and $ {\bf\hat{n}}=({\bf r_1}-{\bf r_2})/\sigma$ is the unit vector along the line of centers $ {\bf r}_1$ and $ {\bf r}_2$ of the colliding disks at contact. With these rules satisfied, the post-collisional velocities are:

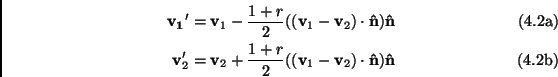\begin{subequations}\begin{align}{\bf v_1}' &={\bf v}_1-\frac{1+r}{2}(({\bf v}_1... ...bf v}_1-{\bf v}_2) \cdot {\bf\hat{n}}){\bf\hat{n}} \end{align}\end{subequations}

In addition, the particles experience the external gravitational field and the presence of confining walls. With respect to the previous Chapter, the energy necessary to prevent the cooling of the system due to the inelastic collisions is not provided by a heat bath: in the present Chapter the energy feeding mechanism is of two types according to the two numerical experiments we perform.

next up previous contents
Next: The boundary conditions of Up: The models Previous: The models   Contents
Andrea Puglisi 2001-11-14