Self-diffusion and time self-correlation in 2D

In Fig. fig_selfdiffusion we report the results of the observation of the average square distance walked by a particle versus time:

$$L(t) = \langle \vert\mathbf{r}(t)-\mathbf{r}(t_0)\vert^2 \rangle$$ (3.19)

where $t_0$ is taken large enough ( $t_0 > \max(\tau_c,\tau_b)$), in order to consider the system time translational invariant (i.e. the initial conditions have been forgotten).

Figure: Averaged square distance $L(t)$ versus time $t$ for different choices of the parameters in $d=2$ DSMC simulations. In all simulations $N=L^2=500$ and $r_B=0.5$. In (a) $T_b=0.01$, in (b) and in (c) $T_b=0.001$. In (d) the same data are rescaled and the initial transient is shown

From the figure it appears that the system presents normal diffusion in both the regimes (colliding and non-colliding), i.e.

$$L(t) \sim 2Dt.$$ (3.20)

The measurement of diffusion coefficients is more interesting. For equilibrium systems the Einstein relation is expected to be satisfied (fluctuation-dissipation relation):

$$D=\tau \langle v^2 \rangle$$ (3.21)

with $\tau$ the typical kinetic relaxation time of the system, $<v(t_1)v(t_2)> \sim \exp(-\vert t_1-t_2\vert/\tau)$. For example, in the case of Brownian motion:

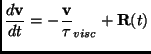$$\frac{d\mathbf{v}}{dt}=-\frac{\mathbf{v}}{\tau}_{visc}+\mathbf{R}(t)$$ (3.22)

with Gaussian white noise $\mathbf{R}(t)$, it happens that $\tau \equiv \tau_{visc}$.

In the collisionless regime, where the heat bath dominates the dynamics, the diffusion coefficient $D$ satisfies the Einstein relation with the bath temperature and $\tau=\tau_b$, as expected.

One may expect that the characteristic relaxation time in the colliding regime ( $\tau_c \ll \tau_b$) is $\tau_c$, but the measurement of the diffusion coefficient shows that this is not the case. In general the diffusion coefficient is somehow very much larger than that expected from this prediction. For the case shown in Fig. fig_selfdiffusion, the time $\tau=D/\langle v^2 \rangle$ is compatible with $\tau_b \gg \tau_c$.

Furthermore the study of the elastic colliding regime, where $\tau_c \ll \tau_b$ but $r=1$ shows that $\tau=\tau_b$.

Figure: Rescaled self-correlation of velocity $\Phi (t)/\Phi (0)$ versus time $t$ for different choices of the parameters in $d=2$ DSMC simulations. In all simulations $N=L^2=500$ and $r_B=0.5$. In (a) $T_b=0.01$, in (b) and in (c) $T_b=0.001$. In (d) the same data are rescaled and the initial transient is shown

These measurements are in agreement with the time self-correlation of velocity:

$$\Phi(t)=<v_x(t_1)v_x(t_1+t)>$$ (3.23)

which is shown in Fig. fig_selfcorr. In all the cases presented an exponential decay is observed:

$$\Phi(t) \sim \exp(-t/\tau)$$ (3.24)

The characteristic relaxation times $\tau$ for the various cases are compatible with the ones measured by means of the relation (3.22). Remarkably, the relaxation time of the colliding regime (elastic or inelastic) is almost equal to $\tau _b$. The slight difference that distinguishes these regimes from the collisionless regime is in the short time behavior of $\Phi(t)$. The fit shown in the Figure is of the kind:

$$\Phi(t)=A \exp(-t/\tau_{short}) + B \exp(-t/\tau_{long})$$ (3.25)

where $\tau_{long} \approx \tau_b$, while $\tau_{short} \approx \tau_b$. The long tails observed in the colliding case (elastic and inelastic) must not be regarded as equivalent to the well known long tails (which are algebraic) measured in elastic hard objects systems (Alder-Wainright, etc.), but as a consequence of the fact that the gas is not at equilibrium. In both elastic and inelastic cases, the particles have a collision rate which is far shorter than the relaxation time due to viscosity. On the other hand the viscosity has a far larger effect on the velocities, as it drags systematically the system toward the absence of flow. It happens that the viscous slow decay dominates the behavior of the self-correlation after a few collision times, while the very first decay is more rapid.

Finally we note that the differences between the relaxation time $\tau$ measured in diffusion and that measured in the self-correlation of velocity, appearing in the inelastic colliding regime, are due to some violation of fluctuation-dissipation relations, which are to be expected in systems out of equilibrium.