Profiles with tangential forces

Figure: Normalized number density $n$, dimensionless horizontal velocity $v_x/\sqrt {g_x\sigma _B}$ and dimensionless granular temperature $T_g/(g_x\sigma _B)$ versus dimensionless height $y/\sigma _B$ for the 2D Inclined Channel Model. Here tangential restitution coefficients smaller than one are considered (see text): $N=500$, $N_w \approx 56$, $g_x=1$, $g_y=-2$ (i.e.: the inclination angle $\phi =\pi /6$), $r^n=0.95$, $r^t=0$, $r_w^n=0.95$,$r_w^t=0$

We consider the comparison between our simplified model and the experimental profiles quite satisfactory: this seems to suggest that introducing further physical details should be irrelevant at this description level. However we briefly report the results obtained with a slightly modified version of the model, including the effects of tangential forces. Such forces play a key role in dense granular flows, e.g. being responsible for arching. On the other hand the present results suggest that in the case of diluted systems they act similarly to the normal forces without introducing noticeable effects.

The introduction of tangential forces in the model studied accounts for a new collision rule:

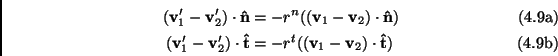where we replace the single restitution coefficient with a pair of parameters $r^n$ and $r^t$, respectively due to the effect of normal and tangential collision forces ($\hat{t}$ is a unit vector perpendicular to $\hat{n}$). Analogously, the restitution coefficient $r_w$ splits in two new parameters $r_w^n$ and $r_w^t$. The results of simulations with several choices of the enlarged set of parameters do not show qualitative differences from the results previously presented: setting tangential restitution coefficients lower than one is equivalent to enhance the dissipation in the original model.

Just as an example of this, we show Fig. fig:c_prof1_bis, where the extremal case of a vanishing tangential restitution coefficient is reported. Note that the profiles are similar to those shown in Fig. fig:c_prof2 where a low $r_w=0.4$ was used.