Distributions of velocities and velocity gradients

Within the early regime the velocity distribution deviates sensibly from a Maxwell distribution (corresponding to the same average kinetic energy), but displays fatter tails, a phenomenon which mirrors the behavior of the BK [24] model. The existence of these tails seems to be due to the lack of spatial correlations, intrinsically absent at all times in their model, whereas negligible in ours up to $t_c$. When the energy begins to decay as $\tau^{-1}$ the velocity distribution turns Gaussian.

Figure: Distributions of $x$ velocity at different times for the same system with $r=0.2$ and $N=512 \times 512$. The distributions are rescaled in order to have unit variance. The initial distribution is a Gaussian. The distribution becomes broader in the uncorrelated phase (first regime), and then turns back toward a Gaussian. At the late instants (when the correlation length has almost reached the finite size of the system) the distribution is still similar to a Gaussian, but presents asymmetries and peaks.

Vortices are not the only topological defects of the velocity fields. In fact we observe shocks, similarly to recent experiments in rapid granular flows[186]. Shocks have a major influence on the statistics of velocity field, i.e. on the probability distributions of the velocity increments. The probability density function (p.d.f.) of the longitudinal increment

Figure: Probability densities of the longitudinal and transverse velocity increments. The main figure shows the p.d.f. of the velocity gradients ($R=1$). The inset shows the Gaussian shape measured for $R=40$ (larger than $L(t)$ for this simulation: $r=0.2$, $t=620$, system size $2048^2$).

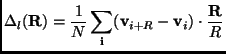$$\Delta_l(\mathbf{R}) = \frac 1N \sum_{\mathbf{i}} (\mathbf {v}_{i+ R} - \mathbf{v}_i) \cdot \frac {\mathbf {R}}{R}$$ (5.73)

is shown in Fig. fig_vgrad for $R=1$ (longitudinal velocity gradient) in the main frame, and for $R=40>L(t)$ in the inset. For small $R\ll L(t)$ the longitudinal increment p.d.f. is skewed with an important positive tail, whereas for $R\gg L(t)$ it turns Gaussian. The distribution of transverse increments

$$(\mathbf{v}_{i+ R} - \mathbf{v}_i)\times \hat{\mathbf{R}}$$ (5.74)

instead, is always symmetric, but non-Gaussian distributed for small $R$. A similar situation exists in fully developed turbulence [26].