



Next: Flow under gravity acceleration
Up: Granular flows
Previous: Slow vs. rapid granular
Contents
The first tentatives of studying granular media under the point of
view of rheology, i.e. transport properties (discussed in more detail
in section 2.4) have been performed using
typical shear experiments used to probe ordinary fluids. In particular
the Couette geometry has been largely used and is still now an
important tool of investigation.
Figure 1.7:
The experiment of Mueth and coworkers on a Couette cylinder: the paths of the internal forces are evidenced by means of non-invasive X-ray imaging
![\includegraphics[clip=true,width=7cm, height=12cm, keepaspectratio]{couette.ps}](img278.png) |
Even if there were earlier important experimental studies on the flow
properties of granular materials (mainly initiated by
Hagen [104] and Reynolds [187]), the modern
pioneering work on the constitutive behavior of rapid granular flows
was Bagnold's experimental study [8] of wax spheres,
suspended in a glycerin-water-alcohol mixture and sheared in a coaxial
cylinder rheometer (Couette experiment). His main finding was a
constitutive relation between internal stresses and shear rate:
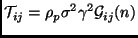 |
(1.13) |
with 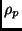 the particle density,
the particle density,  the particle radius,
the particle radius,
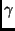 the shear rate and
the shear rate and
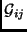 a tensor-valued function
of the solid fraction
a tensor-valued function
of the solid fraction 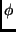 . This relation has been confirmed in
shear-cell experiments with both wet or dry mixtures by Craig et
al. [70], Hanes et al. [105], Savage et
al. [195], and in many computer
simulations [53,54,221].
. This relation has been confirmed in
shear-cell experiments with both wet or dry mixtures by Craig et
al. [70], Hanes et al. [105], Savage et
al. [195], and in many computer
simulations [53,54,221].
Bagnold measured not only shear stresses (i.e. transversal components,
say 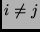 in
in
 ), but also normal stress (
), but also normal stress (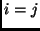 ),
that is the analogous of pressure in gas kinetics: he referred to them
as ``dispersive stresses'' as they tend to cause dilation of the
material.
),
that is the analogous of pressure in gas kinetics: he referred to them
as ``dispersive stresses'' as they tend to cause dilation of the
material.
More recent experiments have focused on different phenomena observed
in the Couette rheometer:
- Fluctuations of stresses: already in the experiments of Savage
and Sayed [195] large fluctuations of internal (normal)
stresses were observed; more recently Howell and
Behringer [113] have seen that in a 2D Couette experiment
the mean internal stress follows a continuous transition when the
packing fraction of the granular material changes and passes through a
critical value
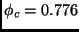 : when the packing fraction is above the
critical threshold the material shows strong fluctuations of internal
stress, while under the threshold the stresses are averagely zero and
the system is highly compressible.
: when the packing fraction is above the
critical threshold the material shows strong fluctuations of internal
stress, while under the threshold the stresses are averagely zero and
the system is highly compressible.
- 3d experiments: Mueth et al. [167] have studied the
formation of microstructures in the dense shearing regime in a 3D
Couette rheometer, using non-invasive imaging by X-Ray microtomography
(see Fig. fig_couette); they have found that the velocity parallel
to the shear direction decays more rapidly than linear (from
exponential to Gaussian-like decay, depending upon the regularity of
the grains). A similar strong decay of the flow with the distance from
the moving wall was observed in many experiments, for example recently
by Losert et al. [145]
- Diluted (air-fluidized) shear: Losert et al. [143]
have performed a Couette experiment with a flow of air coming from the
bottom of the cylinder, in order to fluidize the material and
obtaining smoother profiles. They have put in relation the RMS
fluctuations of velocity and the shear forces, observing that
 with
with
 , and suggesting a
phenomenological model that explains the shear velocity profiles.
, and suggesting a
phenomenological model that explains the shear velocity profiles.
- Size segregation: Khosropour et al. [123] have
observed convection patterns and size segregation in a Couette flow
with spherical glass beads; they also checked the effect of
interstitial fluids finding it irrelevant.
- Planetary rings: planetary rings (those of Saturn
for example) have been sometime studied in the framework of granular
rheology, whereas the ``geometry'' of the planetary experiment is
similar to a Couette cell (grains are circularly sheared because the
angular velocity depends upon the distance from the planet). A review
of these study can be found in the work of Brahic [37].




Next: Flow under gravity acceleration
Up: Granular flows
Previous: Slow vs. rapid granular
Contents
Andrea Puglisi
2001-11-14
![\includegraphics[clip=true,width=7cm, height=12cm, keepaspectratio]{couette.ps}](img278.png)
![\includegraphics[clip=true,width=7cm, height=12cm, keepaspectratio]{couette.ps}](img278.png)
![]() the particle density,
the particle density, ![]() the particle radius,
the particle radius,
![]() the shear rate and
the shear rate and
![]() a tensor-valued function
of the solid fraction
a tensor-valued function
of the solid fraction ![]() . This relation has been confirmed in
shear-cell experiments with both wet or dry mixtures by Craig et
al. [70], Hanes et al. [105], Savage et
al. [195], and in many computer
simulations [53,54,221].
. This relation has been confirmed in
shear-cell experiments with both wet or dry mixtures by Craig et
al. [70], Hanes et al. [105], Savage et
al. [195], and in many computer
simulations [53,54,221].
![]() in
in
![]() ), but also normal stress (
), but also normal stress (![]() ),
that is the analogous of pressure in gas kinetics: he referred to them
as ``dispersive stresses'' as they tend to cause dilation of the
material.
),
that is the analogous of pressure in gas kinetics: he referred to them
as ``dispersive stresses'' as they tend to cause dilation of the
material.